Wie rechnet man eine quadratische Funktion durch Winkel und Punkte aus?

Question

Aufgabe:

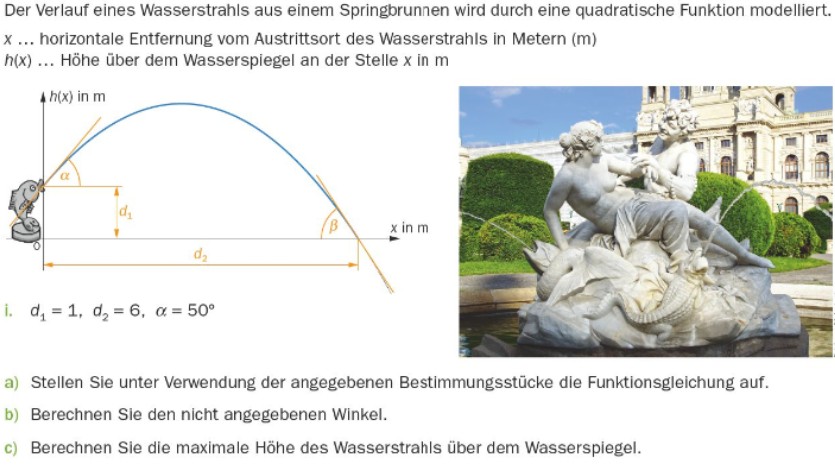
Der Verlauf eines Wasserstrahls aus einem Springbrunnen wird durch eine quadratische Funktion modelliert.

\( x \ldots \) horizontale Entfernung vom Austrittsort des Wasserstrahls in Metern

\( h(x) \ldots \) Höhe über dem Wasserspiegel an der Stelle \( x \) in \( m \)

\( d_{1}=1 \quad d_{2}=6 \quad \alpha=50^{\circ} \)

a) Stellen Sie unter Verwendung der angegebenen Bestimmungsstücke die Funktionsgleichung auf.

b) Berechnen Sie den nicht angegebenen Winkel.

c) Berechnen Sie die maximale Höhe des Wasserstrahls über dem Wasserspiegel.

Problem/Ansatz:

Ich verstehe die ganze Aufgabe nicht. Wäre super wenn mir jemand helfen könnte

Danke im Voraus!

Comments

Auf dem mitgelieferten Bild erkennt man einen Brunnen von Hugo Haerdtl in Wien.

Answer 1

Hallo,

die allgemeine Form einer quadratische Funktion ist$$h(x)=ax^2+bx+c$$aus \(d_1=1\) folgt bereits \(c=d_1=1\). Bei \(d_2\) liegt eine Nullstelle der Funktion. Daraus folgt$$h(d_2=6)= a \cdot 6^2 + b \cdot 6 + 1 = 0$$Dr Winkel bei \(x=0\) ist \(50°\). Damit ist die Steigung in diesem Punkt gegeben$$h'(0) = 2a \cdot 0 + b = \tan(50°) \implies b = \tan(50°) \approx 1,19$$oben eingesetzt ergibt das für \(a\)$$\begin{aligned} 36a + 6\tan(50°) + 1 &= 0\\ 36a &= -6\tan(50°) - 1 \\ a &= -\frac{6\tan(50°) + 1}{36} \approx 0,226\end{aligned}$$Alles zusammen gesetzt$$h(x) \approx -0,226x^2 +1,19x + 1$$Der Winkel \(\beta\) ist$$\beta = - \arctan\left(h'(d_2=6)\right) \approx 56,7°$$

wenn Du noch Fragen hast, z.B. wie man den höchsten Punkt berechnet, so melde Dich bitte.

Gruß Werner

Comments

Dankeschön. Aber ich verstehe nicht ganz wie man auf dem Winkel ß kommt.

Lg

---

Aber ich verstehe nicht ganz wie man auf dem Winkel ß kommt.

Die Steigung einer Funktion ist identisch zum Tangens des Winkels, die die Funktion - bzw. die Tangente der Funktion - zur X-Achse einnimmt. Gefragt ist aber nach dem Scheitelwinkel des eigentliches 'Richtungswinkel'. Und da die Steigung bei \(d_2\) negativ ist, wird ersterer positiv.

Und aus$$h'(d_2) = \tan(-\beta)$$folgt dann $$\beta = -\arctan(h'(d_2))$$und \(h'(d_2)\) ist$$h'(x)= 2ax + b \\ h'(d_2=6) \approx 2\cdot (-0,226) \cdot 6 + 1,19 \approx -1,525$$