Gegeben seien Matrizen B und A über demselben Körper K, die in der unten angegebenen Form
aus lm bzw. mn Teilmatrizen zusammengesetzt sind. Derartige Matrizen werden Blockmatrizen genannt.
Beweise
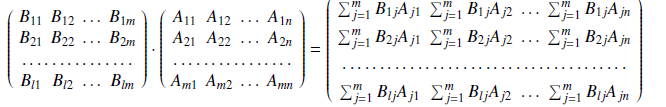
unter der Voraussetzung, dass alle rechts vom Gleichheitszeichen angeschriebenen Matrizenprodukte
definiert sind. Was bedeutet diese Voraussetzung für die Zeilen- bzw. Spaltenanzahl der einzelnen Teilmatrizen?
Bemerkung: Das Produkt geeignet unterteilter Blockmatrizen kann also selbst wie ein Matrizenprodukt
berechnet werden.
Soll man hier einfach stumpf nachrechnen oder wie geht man hier vor? Wüsste nicht ganz weiter