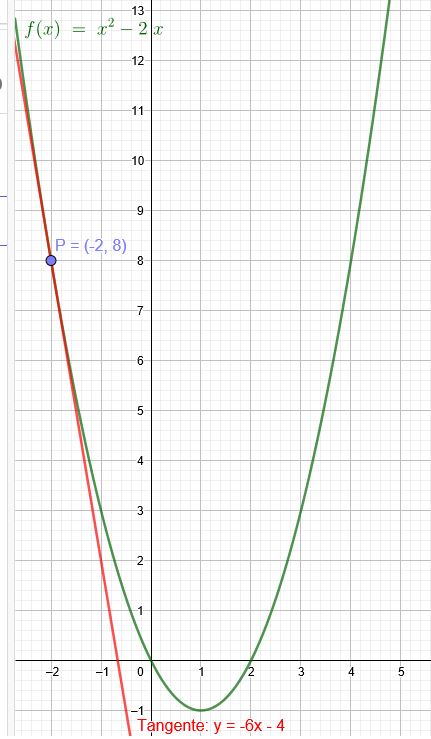
Bestimmen Sie die Steigung von \(y = x^2 - 2 x\) im Punkt \(P (-2|8)\)
Weg ohne Ableitung:
\( \frac{y-8}{x-(-2)}=m \) \( \frac{y-8}{x+2}=m \)
\(y=m*(x+2)+8 \)
\( x^2 - 2 x=m*x+2m+8\) → \( x^2 - 2 x-m*x=2m+8\)
\( x^2 -(2+m)*x=2m+8\)
\( (x -\frac{2+m}{2})^2=2m+8+\frac{4+4m+m^2}{4}=\frac{8m+32+4+4m+m^2}{4}=\frac{m^2+12m+36}{4}=\frac{(m+6)^2}{4}|\sqrt{~~}\)
Bei einem Schnittpunkt muss der Term unter der Wurzel =0 sein:
\( \frac{(m+6)^2}{4} =0\)
\(m=-6\)