In diesem Forum stand gestern diese Aufgabe:
‚Setzt man an einer Grundstücksgrenze einen Zaun mit einem Pfostenabstand von 1,2m, benötigt man 16 Pfosten. Die Pfosten sollen nur 0,90 m voneinander entfernt sein. Wie viele Pfosten benötigt man nun? Fertige zunächst eine Skizze an.‘
Alle Antworten (meine eingeschlossen) und Kommentare haben nicht berücksichtigt, dass bei Grundstückszäunen Pfosten genau auf den Ecken des Grundstücks stehen müssen. Mit 16 Pfählen muss für die Eckenzahl n des Grundstücks gelten 3≤n≤16. Das größte Grundstück, das dann von einem Zaun mit 16 Pfählen (Pfahlabstand 1,2 m) umzäunt werden kann ist ein Grundstück von der ungewöhnlichen Form eines regelmäßigen 16-Ecks und der ungewöhnlichen Grundstücksgröße von ungefähr 29 m2. Ein quadratisches Grundstück der in der Aufgabe genannten Art hätte eine Größe von ungefähr 23 m2. Dazu folgende Abbildung:
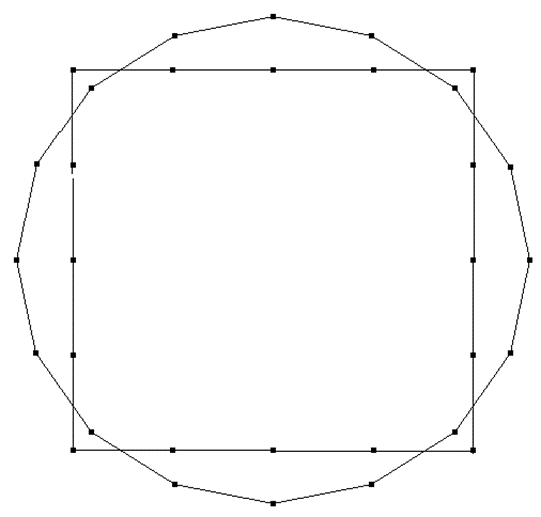
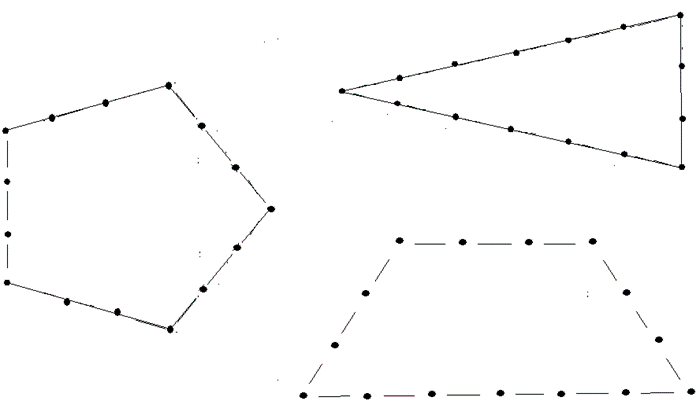
Bei keinem dieser Grundstücke könnte der Pfahlabstand 0,9 m sein. Denn auf jedem Zaunabschnitt mit 1,2 m Pfahlabstand, der keine Ecke aufweisen darf, werden statt der drei Pfähle jetzt 4 Pfähle nach Verkürzung des Pfahlabstandes auf 0,9 m untergebracht. Damit muss die Anzahl der Pfähle mit größerem Pfahlabstand durch 3 teilbar sein, wenn der Zaun das ganze Grundstück umschließt. Auch jeder Zaunabschnitt von Ecke zu Ecke mit 1,2 m Pfahlabstand muss eine um 1 erhöhte durch 3 teilbare Anzahl von Pfählen aufweisen. Beides ist für 16 aber nicht der Fall. Hätte der Zaun statt 16 Pfähle nur 15 Pfähle gehabt, hätte das Grundstück nur ein gleichschenkliges Dreieck, ein trapezförmiges Viereck oder ein gleichseitiges Fünfeck sein können.