( 7 - 6x )/( 3x + 8) ≤ 0
Bitte nach folgendem Schema mit einfachen, nachvollziehbaren Erklärungen:
- Definitionsmenge bestimmen
Nenner ≠0
3x+8≠0
3x≠-8
x ≠ -8/3
- Fallunterscheidungen ( 1 und 2 )
1. Fall x > -8/3
( 7 - 6x )/( 3x + 8) ≤ 0 |Hauptnenner > 0
( 7 - 6x ) ≤ 0
7 ≤ 6x
7/6 ≤ x
x muss also grösser als -8/3 und grösser oder gleich 7/6 sein. Es genügt zu verlangen, das x≥7/6 ist.
L1 = {x|x ≥ 7/6}
2. Fall x < -8/3
( 7 - 6x )/( 3x + 8) ≤ 0 |Hauptnenner < 0
( 7 - 6x ) ≥ 0
7 ≥ 6x
7/6 ≥ x
Hier ist x<-8/3 die strengere Einschränkung
L2 = {x|x < -8/3}
- Ungleichungen für beide Fälle vgl. oben.
- Gesamtlösungsmenge bestimmen
L = L1 u L2 = {x| x<-8/3 oder x ≥ 7/6}
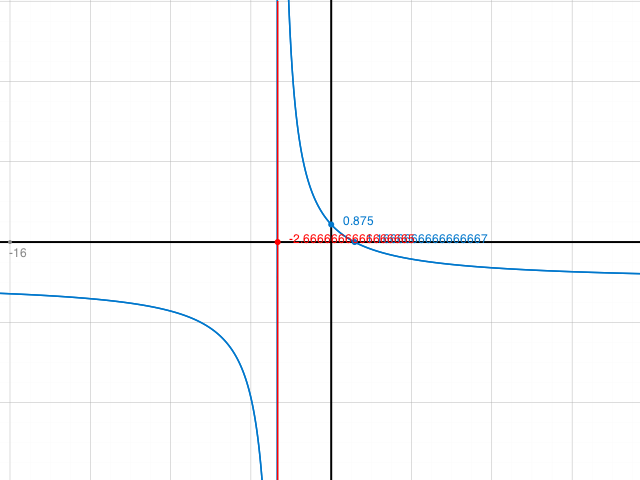
Links von -2.6666667 und ab 1.1666666 gegen rechts ist der Bereich, in dem die Kurve nicht über der x-Achse verläuft.
x = -8/3 ist die Polstelle und x = 7/6 die Nullstelle der Funktion f(x) = ( 7 - 6x )/( 3x + 8)