Aufgabe:
Text erkannt:
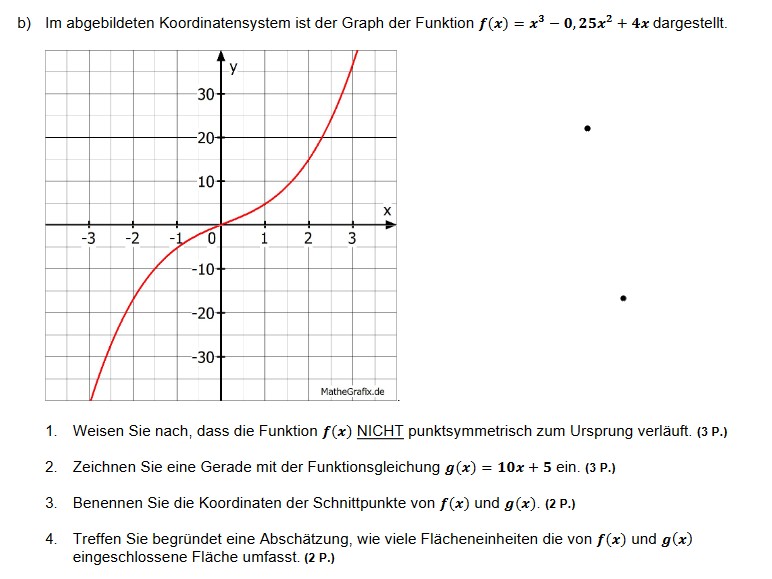
b) Im abgebildeten Koordinatensystem ist der Graph der Funktion \( f(x)=x^{3}-\mathbf{0}, \mathbf{2 5} \boldsymbol{x}^{2}+\mathbf{4} \boldsymbol{x} \) dargestellt.
1. Weisen Sie nach, dass die Funktion \( \boldsymbol{f}(\boldsymbol{x}) \) NICHT punktsymmetrisch zum Ursprung verläuft. (3 P.)
2. Zeichnen Sie eine Gerade mit der Funktionsgleichung \( g(x)=10 x+5 \) ein. (3 P.)
3. Benennen Sie die Koordinaten der Schnittpunkte von \( \boldsymbol{f}(\boldsymbol{x}) \) und \( \boldsymbol{g}(\boldsymbol{x}) \). (2 P.)
4. Treffen Sie begründet eine Abschätzung, wie viele Flächeneinheiten die von \( \boldsymbol{f}(\boldsymbol{x}) \) und \( \boldsymbol{g}(\boldsymbol{x}) \) eingeschlossene Fläche umfasst. (2 P.)
Problem/Ansatz:
1) und 2) sind mir klar. Jedoch scheint mir die Lösung von f(x) = g(x) für die Aufgabe 3) ziemlich komplex zu sein, das Schlüsselwort "Bennenen" in der Aufgabenstellung vermittelt mir den Eindruck, dass man auch ohne Rechnung eine Antwort auf die Frage geben kann, gleiches gilt für die Aufgabe 4) - ohne eine Integration sollte auch hier eine Antwort möglich sein? Leider habe ich hier bisher keinen Lösungsansatz (abgesehen vom tatsächlichen Rechnen gefunden).