Zeigen Sie dass dann \langle x, y\rangle_{D}:=x^{T} · D · y ein Skalarprodukt auf ℝ^{n} definiert.

Question

Aufgabe: Skalarprodukt auf R hoch n definiert zeigen

Problem/Ansatz: Habe kein Plan wie ich das machen soll, könnte mir da jemand vlt helfen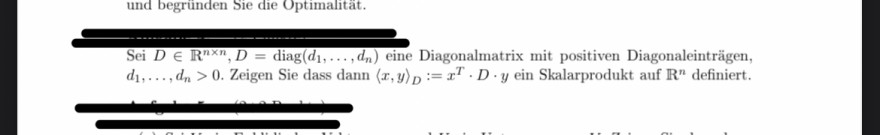

Text erkannt:

und begründen Sie die Optimalität.
Sei \( D \in \mathbb{R}^{n \times n}, D=\operatorname{diag}\left(d_{1}, \ldots, d_{n}\right) \) eine Diagonalmatrix mit positiven Diagonaleinträgen, \( d_{1}, \ldots, d_{n}>0 \). Zeigen Sie dass dann \( \langle x, y\rangle_{D}:=x^{T} \cdot D \cdot y \) ein Skalarprodukt auf \( \mathbb{R}^{n} \) definiert.

Comments

Habe kein Plan wie ich das machen soll

Prüfe die Eigenschaften eines Skalarproduktes.
Welche Eigenschaften ein Skalarprodukt definieren,
solltest du in deinen Unterlagen finden:

du musst zeigen, dass es sich um eine positiv-definite
symmetrische Bilinearform handelt.