dim_k soll ja heißten, dass es endlich ist, oder?

Question

Aufgabe:

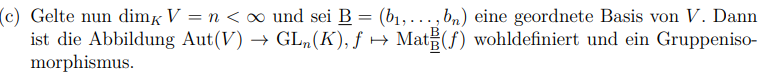
Text erkannt:

(c) Gelte nun \( \operatorname{dim}_{K} V=n<\infty \) und sei \( \underline{\mathrm{B}}=\left(b_{1}, \ldots, b_{n}\right) \) eine geordnete Basis von \( V \). Dann ist die Abbildung \( \operatorname{Aut}(V) \rightarrow \mathrm{GL}_{n}(K), f \mapsto \operatorname{Mat}_{\underline{\mathrm{B}}}(f) \) wohldefiniert und ein Gruppenisomorphismus.

Problem/Ansatz:

dim_k soll ja heißten, dass es endlich ist, oder? normalerweise schreibt man es, aber hier wurde es versucht so zu zeigen oder?

Wo ist der zsmhang zwischen geordneten Basen und wohldefiniertheit? sind bei geordnete Basen nicht es dann injektiv und damit nicht wohldefiniert oder ist es bijektiv und ich erkenne es nicht?

und Gruppenhormo. kann ich beweisen in dem ich zeige, dass es eine lineare Abbildung ist oder?

Comments

\(\dim_K V\) bedeutet nur, dass man den Vektorraum bzgl. des Körpers \(K\)  betrachtet.

Zum Beispiel ist \(\dim_{\mathbb{C}}C = 1\) aber \(\dim_{\mathbb{R}}C = 2\).

Die Festlegung auf eine geordnete Basis sorgt dafür, dass es genau eine Matrix für eine lineare Abbildung gibt und nicht mehrere, die durch Umordnen der Basisvektoren entstehen.