Bestimme die Schnittpunkte des Graphen von f mit den Koordinatenachsen.

Question

Aufgabe:

Gegeben ist die Funktion f mit f(x)=(x^2-2x)•e^0.5x

a) Bestimme die Schnittpunkte des Graphen von f mit den Koordinatenachsen.

b) Bestimme die Extrem- und Wendepunkte des Graphen von f

c) Bestimme die Gleichung der Tangente im Koordinatenursprung

Problem/Ansatz:

Hallo Leute, ich brauche eure Hilfe bei dieser Aufgabe. Würdet ihr mir netterweise den Lösungsweg zu diese Aufgaben sagen. Denn ich verstehe überhaupt nicht, was von mir verlangt ist.

Answer 1

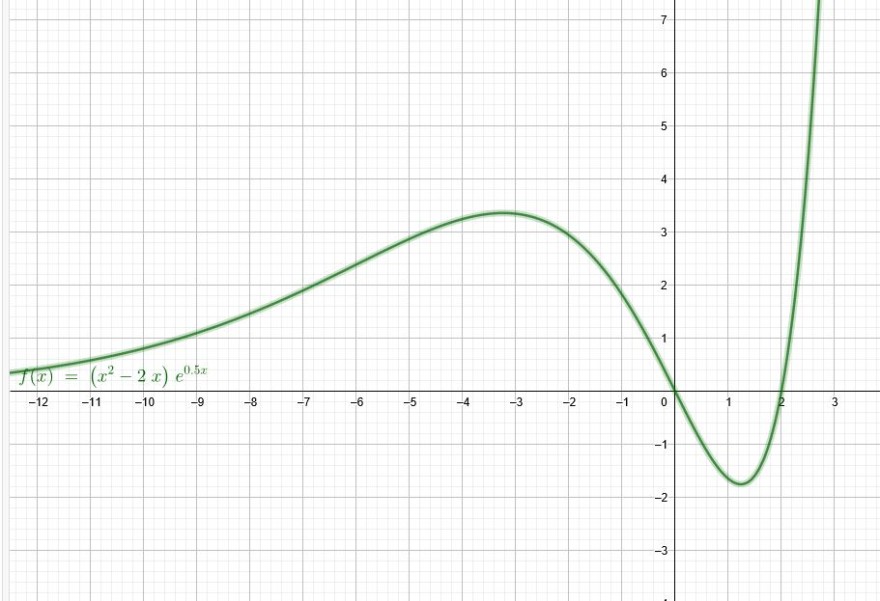
\(f(x)=(x^2-2x)•e^{0,5x}\)

a) Bestimme die Schnittpunkte des Graphen von f mit den Koordinatenachsen.

Nullstellen:

\((x^2-2x)•e^{0,5x}=0\)     \((x^2-2x)=0\)     \(x₁=0∨x₂=2\)      \(e^{0,5x}≠0\)

Schnitt mit y-Achse:

\(f(0)=(0^2-2*0)•e^{0,5*0}=0\)

b) Bestimme die Extrem- und Wendepunkte des Graphen von f

Extremwerte:

\(f´(x)=(2x-2)•e^{0,5x}+(x^2-2x)*e^{0,5x}*0,5=e^{0,5x}*(2x-2+x^2-2x)=e^{0,5x}*(x^2-2)\)

\(e^{0,5x}*(x^2-2)=0\)        \((x^2-2)=0\)       \(x₁=\sqrt{2}∨x₂=-\sqrt{2}\)  Beide y-Werte noch bestimmen.

Art des Extremwertes:

\(f´´(x)=e^{0,5x}*0,5*(x^2-2)+e^{0,5x}*2x=e^{0,5x}*(0,5x^2-1+2x)\)

\(f´´(\sqrt{2})=e^{0,5*\sqrt{2}}*(0,5*2-1+2*\sqrt{2})>0\) Minimum

\(f´´(-\sqrt{2})\)=....

Comments

Danke sehr :)

Answer 2

a) f(0) = .. (y-Achse)

f(x) = 0 (x-Achse)

b) Ableiten mit der Produktregel!

Extrema: f '(x) =0

Wendepunkt: f ''(x) = 0 

c) t(x) = (x-0)*f '(0) + f(0)

Comments

Vielen Dank :)

Answer 3

f ( x ) =(x^2-2*x) • e^(0.5x)

a) Bestimme die Schnittpunkte des Graphen von f mit den Koordinatenachsen.

Schnittpunkt mit der x-Achse : y = 0
(x^2-2*x) • e^(0.5x) = 0
Satz vom Nullprodukt anwenden
x^2 - 2*x = 0
x *  ( x - 2 ) = 0
x = 0
und x = 2

( 0 | 0 )
( 2 | 0 )

e^(0.5x) kann nie null werden

Schnittpunkt mit der y-Achse : x = 0
y = (0^2-2*0) • e^(0.5*0) = 0
y = 0
( 0  | 0 )

Bei Bedarf weiterfragen.

Comments

Dankeschön :)

Answer 4

c) Die erste Ableitung an der Stelle 0 ist die Steigung m der Tangente y=mx. Wegen m=.2 ist die gesuchte Tangentengleichung y=-2x..

Comments

Dankeschön. Kannst du mir auch bitte mit b helfen?

---

Was genau ist dein Problem bei b)? Welche Hilfsmittel dürft ihr benutzen?