Zeigen Sie für k ∈ ℕ : lim

Question

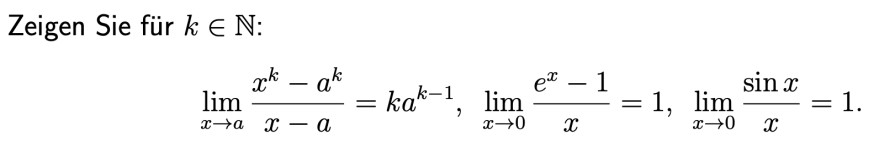
Text erkannt:

Zeigen Sie für \( k \in \mathbb{N} \) :
\( \lim \limits_{x \rightarrow a} \frac{x^{k}-a^{k}}{x-a}=k a^{k-1}, \lim \limits_{x \rightarrow 0} \frac{e^{x}-1}{x}=1, \lim \limits_{x \rightarrow 0} \frac{\sin x}{x}=1 \)

Ansatz wäre Sin(x) und e^x als Potenzreihen schreiben

Hey, liebe Mathelounge Community, ich bräuchte mal eure Hilfe

komme leider nicht weiter, könnte wer mir bitte vorrechnen. LG

Answer 1

Für differenzierbare Funktionen gilt:

\(\lim_{x\to a}\frac{f(x) - f(a)}{x-a} = f'(a)\)

\((1) f(x) = x^k\)

\((2) f(x) = e^x, a = 0\)

\((3) f(x) = \sin x, a = 0\)

Answer 2

Eine andere Möglichkeit ist, L'Hosptal zu verwenden.
Das führt rasch zum Ziel.