Aufgabe: Untersuchen Sie, welche der folgenden Grenzwerte existieren. Bestimmen Sie gegebenenfalls ihren Wert.
Könnte jemand meine Lösung korrigieren :) ?
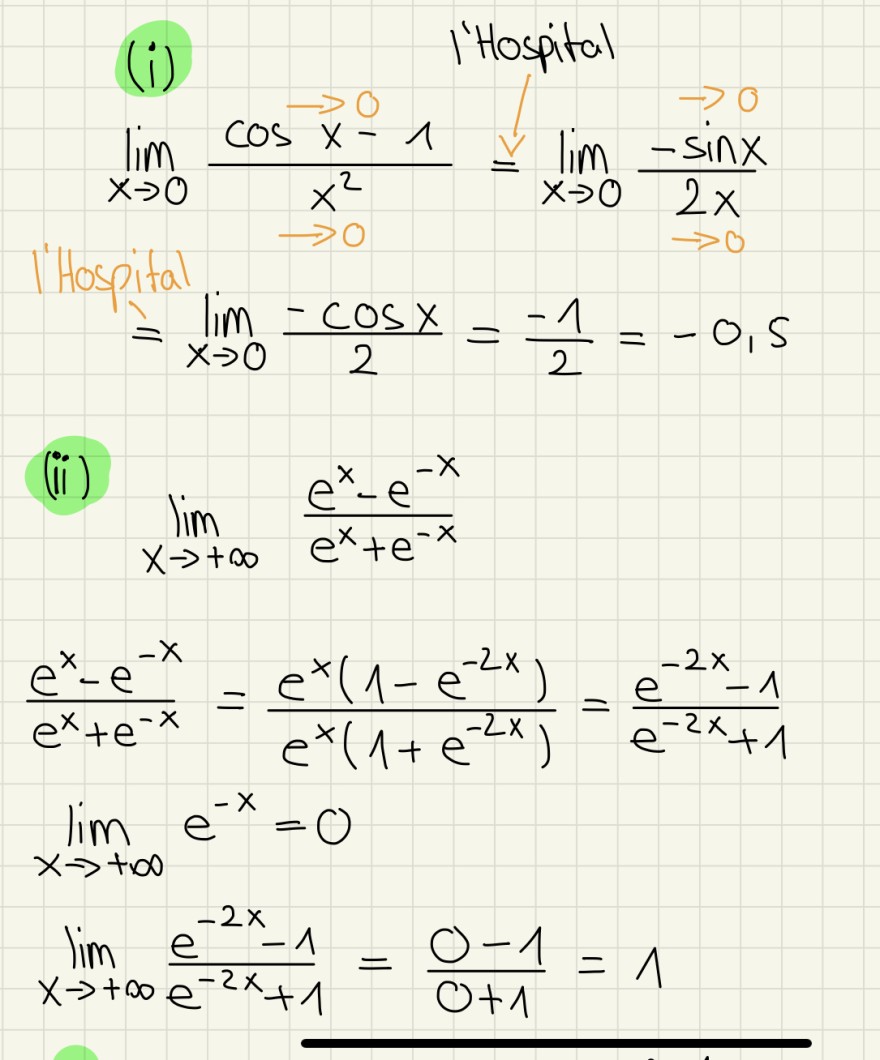
Text erkannt:
(i) \( \operatorname{limospital~}_{x \rightarrow 0} \frac{\cos x-1}{x^{2}}=\lim \limits_{x \rightarrow 0} \frac{-\sin x}{2 x} \)
I'Hospital \( \rightarrow \lim \limits_{x \rightarrow 0} \frac{-\cos x}{2}=\frac{-1}{2}=-0,5 \)
(ii) \( \lim \limits_{x \rightarrow+\infty} \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} \)
\( \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}=\frac{e^{x}\left(1-e^{-2 x}\right)}{e^{x}\left(1+e^{-2 x}\right)}=\frac{e^{-2 x}-1}{e^{-2 x}+1} \)
\( \lim \limits_{x \rightarrow+\infty} e^{-x}=0 \)
\( \lim \limits_{x \rightarrow+\infty} \frac{e^{-2 x}-1}{e^{-2 x}+1}=\frac{0-1}{0+1}=1 \)
Problem/Ansatz:
Weiß nicht ob es richtig ist