Die Verteilungsfunktion ist definiert durch \(F_Z(z) =P(Z\leq z)\).
Wenn K für Kopf und W für Wappen steht, gilt $$\begin{array}{rcl}F_Z(z) & = & P(Z\leq z) \\ & = & P(Z\leq z|K)\cdot P(K) + P(Z\leq z|W)\cdot P(W)\\ & = & \frac 12 P(Z\leq z|K) + \frac 12 P(Z\leq z|W)\end{array}$$
Dabei sind \(P(Z\leq z|K)\) und \(P(Z\leq z|W)\) die Verteilungsfunktion der Gleichverteilung auf [1,3] bzw. [2,4]. Also
$$P(Z\leq z|K) = \left\{ \begin{array}{cc} 0 & z<1 \\ \frac{z-1}{2} & 1 \leq z < 3 \\ 1 & z \geq 3 \end{array}\right.$$
$$P(Z\leq z|K) = \left\{\begin{array}{cc} 0 & z<2 \\ \frac{z-2}{2} & 2 \leq z < 4 \\ 1 & z \geq 4 \\ \end{array}\right.$$
Damit erhältst du
$$F_Z(z)=\left\{ \begin{array}{cc} 0 & z<1 \\ \frac{z-1}{4} & 1\leq z<2 \\ \frac{1}{4} (2 z-3) & 2 \leq z < 3 \\ \frac{z}{4} & 3\leq z < 4 \\ 1 & z \geq 4 \\ \end{array}\right.$$
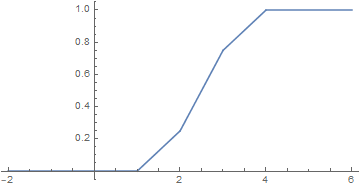
Die Dichte \(f_Z(z)\) erhältst du durch Ableiten der Verteilungsfunktion innerhalb der Intervalle. An den Endpunkten 1,2,3,4 existiert die Ableitung nicht und kann beliebig gesetzt werden, da dies bei der Integration über die Dichte keine Rolle spielt:
$$f_Z(z) = \left\{\begin{array}{cc} 0 & z<1 \\ \frac{1}{4} & 1\leq z<2 \\ \frac{1}{2} & 2 \leq z<3 \\ \frac{1}{4} & 3\leq z<4 \\ 0 & z>4 \end{array}\right.$$
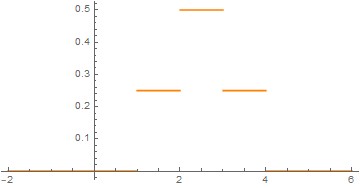
Zum Schluss:
$$\begin{array}{rcl} E(Z^3) & = & \int_{-\infty }^{\infty } z^3 f_Z(z) \, dz \\ & = & \frac 14 \int_{1}^{2} z^3 \, dz + \frac 12 \int_{2}^{3} z^3 \, dz + \frac 14 \int_{3}^{4} z^3 \, dz \\ & = & 20\end{array}$$
$$$$