Aufgabe:
1. Vereinfache mithilfe Potenzgesetze
2. Verfahre wie im Beispiel (siehe Bild)
Problem/Ansatz:
Hi! Bei der zweiten Aufgabe weiß sich nicht wie ich weiter rechnen soll, bei der ersten steht das Ergebnis solle ein anderes sein, ich verstehe nicht wieso dies 9/8y und nicht 3/8y 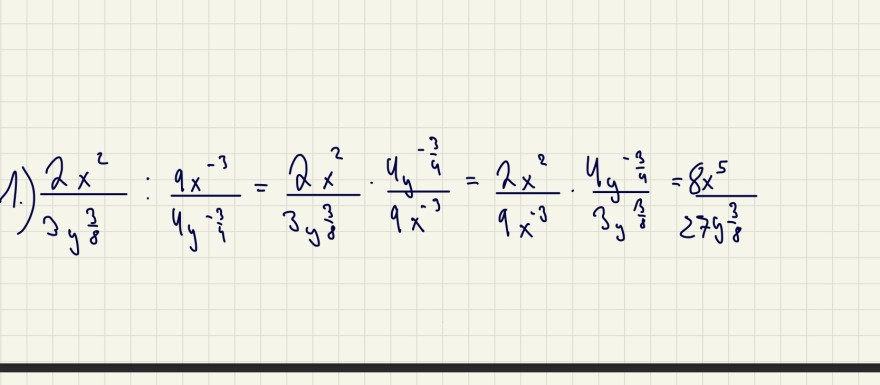
Text erkannt:
1.) \( \frac{2 x^{2}}{3 y^{\frac{3}{8}}}: \frac{9 x^{-3}}{4 y^{-\frac{3}{4}}}=\frac{2 x^{2}}{3 y^{\frac{3}{8}}} \cdot \frac{4_{y}^{-\frac{3}{4}}}{9 x^{-3}}=\frac{2 x^{2}}{9 x^{-3}} \cdot \frac{4 y^{-\frac{3}{4}}}{3 y^{\frac{3}{8}}}=\frac{8 x^{5}}{27 y^{\frac{3}{8}}} \)
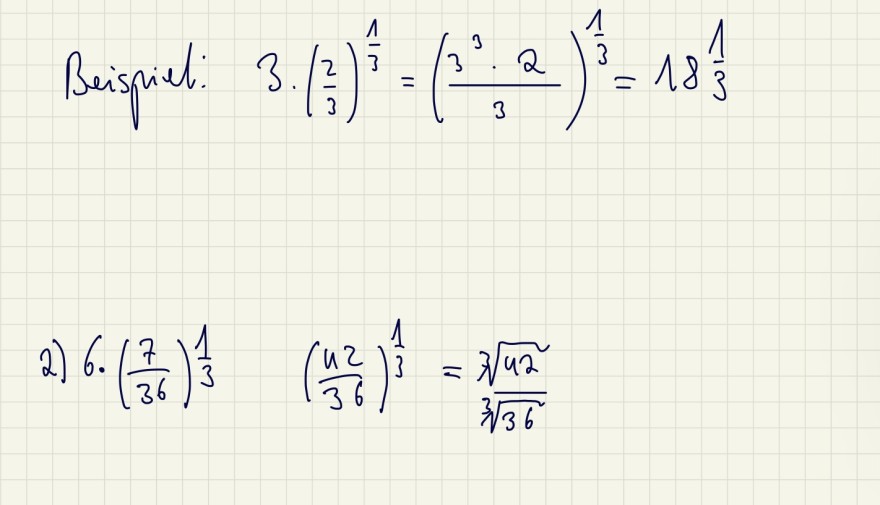
Text erkannt:
Beispiel: \( \quad 3 \cdot\left(\frac{2}{3}\right)^{\frac{1}{3}}=\left(\frac{3^{3} \cdot 2}{3}\right)^{\frac{1}{3}}=18 \frac{1}{3} \)
2) \( 6 \cdot\left(\frac{7}{36}\right)^{\frac{1}{3}} \quad\left(\frac{42}{36}\right)^{\frac{1}{3}}=\frac{\sqrt[3]{42}}{\sqrt[3]{36}} \)
ist.