Beschränktheit und Konvergenz beweisen

Question

Aufgabe:

Unterstrichene Folge soll auf Konvergenz und Beschränktheit untersucht und bewiesen werden..

Text erkannt:

nufgabe 29 zeschrannutneit, konvergenz \& Divergenz
a) $\left(a_{n}\right)_{n \in \mathbb{N}}$ mit $a_{n}:=\frac{2^{n-1}}{n^{3}+42}-5_{n}$

Problem/Ansatz:

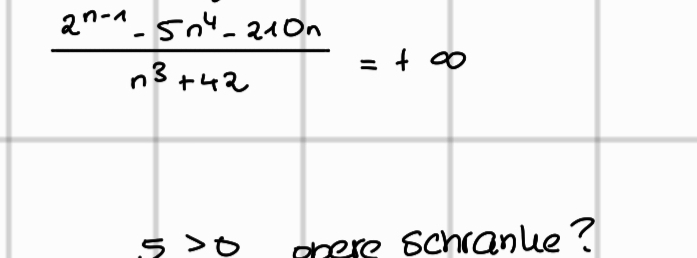
Text erkannt:

$\frac{2^{n-1}-5 n^{4}-210 n}{n^{3}+42}=+\infty$

Meine Überlegungen war, dass wenn man 5n auf den Bruch bekommt, der Zählergrad größer ist und due Funktion somit gegen Unendlich konvergiert.

Bei der Beschränkung bin ich mir auch unsicher..

Wie muss man da genau vorgehen :/ ??

Answer 1

2^(n-1) wächst am schnellsten und entscheidet.