Aufgabe: Welche der Funktionen ist injektiv?
⇤ f : N -> Z/113, f(n) := n mod 113,
⇤ f : Z/22 -> Z/22, f(n) := (4n) mod 22,
⇤ f : Z -> N, f(n) := n^2 + 1.
Problem/Ansatz:
Ich komme auf das Ergebnis, dass keiner dieser Funktionen injektiv ist. Das finde ich etwas merkwürdig...
Bei der ersten Funktion hat ja für n=113 und n=226 beide 0 als y wert somit nicht injektiv.
Bei der zweiten Funkktion für n=1 und für n=12 beide 4 als y wert, somit auch nicht injektiv
Bei der dritten, sowohl n=4 und und n=-4 beide 17 als y wert, somit auch nicht injektiv.
Habe ich irgendwo ein denkfehler?
Vielen Dank!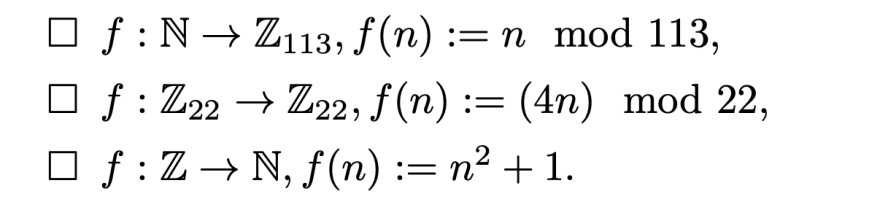
Text erkannt:
\( f: \mathbb{N} \rightarrow \mathbb{Z}_{113}, f(n):=n \bmod 113 \)
\( f: \mathbb{Z}_{22} \rightarrow \mathbb{Z}_{22}, f(n):=(4 n) \bmod 22 \),
\( f: \mathbb{Z} \rightarrow \mathbb{N}, f(n):=n^{2}+1 \)