Tangens und Kotangens, Periode und Symmetrie

Question

Aufgabe:

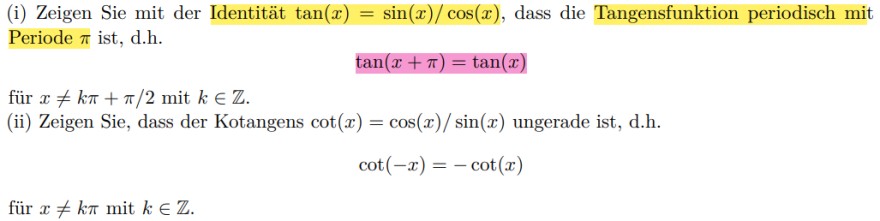
Text erkannt:

(i) Zeigen Sie mit der Identität \( \tan (x)=\sin (x) / \cos (x) \), dass die Tangensfunktion periodisch mit Periode \( \pi \) ist, d.h.
\( \tan (x+\pi)=\tan (x) \)
für \( x \neq k \pi+\pi / 2 \) mit \( k \in \mathbb{Z} \).
(ii) Zeigen Sie, dass der Kotangens \( \cot (x)=\cos (x) / \sin (x) \) ungerade ist, d.h.
\( \cot (-x)=-\cot (x) \)
für \( x \neq k \pi \) mit \( k \in \mathbb{Z} \).

Problem/Ansatz:

1) \(tan(x+pi) = \frac {sin(x+pi)}{cos(x+pi)} = \frac{-sin(x)}{-cos(x)} = \frac{sin(x)}{cos(x)} = tan(x)\)

2) \( cot(-x) = \frac{cos(-x)}{sin(-x)} = \frac{cos(x)}{-sin(x)} = -cot(x)\)

Stimmt das so oder muss man noch mehr machen?

Answer 1

Stimmt das so oder muss man noch mehr machen?

Das stimmt so. Gut gemacht.

Comments

Danke Dir fürs drüber schauen!

Answer 2

Zeigen Sie mit der Identität \( \tan (x)=\sin (x) / \cos (x) \), dass die Tangensfunktion periodisch mit Periode \( \pi \) ist, d.h.\( \tan (x+\pi)=\tan (x) \)

\( \tan (x+\pi)=\frac{\sin (x+\pi) }{\cos(x+\pi) } =  \frac{-\sin (x) }{-\cos(x)}= \tan (x) \)