Bestimme die Menge aller Häufungspunkte der gegebenen Folge:

Question

Aufgabe: Bestimme die Menge aller Häufungspunkte der gegebenen Folge:

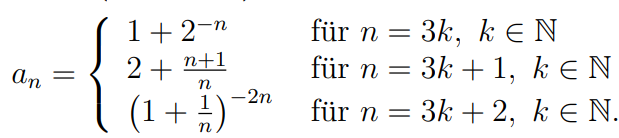
Text erkannt:

\( a_{n}=\left\{\begin{array}{ll}1+2^{-n} & \text { für } n=3 k, k \in \mathbb{N} \\ 2+\frac{n+1}{n} & \text { für } n=3 k+1, k \in \mathbb{N} \\ \left(1+\frac{1}{n}\right)^{-2 n} & \text { für } n=3 k+2, k \in \mathbb{N} .\end{array}\right. \)

Problem/Ansatz:

Ich verstehe nicht warum drei Folgen in einer Folge gegeben sind. Sollen das Teilfolgen sein ? Da ich bisher mit einer Folge gearbeitet hatte, komme ich bei dieser Aufgabe nicht voran. Ich bitte daher um einen Lösungsvorschlag oder Ansatz.

Vielen Dank im Voraus!

Answer 1

\(\text { für } n=3 k, k \in \mathbb{N}\)

Damit ist gemeint:

        falls ein \(k \in \mathbb{N}\) existiert, so dass \(n = 3k\) ist.

warum drei Folgen in einer Folge gegeben sind.

Weil der Autor der Aufgabe das so wollte.

Sollen das Teilfolgen sein ?

Es sind Teilfolgen. Und zwar unabhängig davon was es sein sollen.

Ein paar Beispiele, wie die Notation zu lesen ist:

1. Es ist

           \(a_{17} = \left(1+\frac{1}{17}\right)^{-2\cdot 17}\)
   

   weil ein \(k \in \mathbb{N}\) existiert, so dass

           \(n = 3k+2\)
   

   ist (nämlich \(k = 5\)).
   

2. Es ist

     \(a_{528} = 1+2^{-528}\)

   weil ein \(k \in \mathbb{N}\) existiert, so dass

     \(n = 3k\)

   ist (nämlich \(k = 176\)).

3. Es ist

     \(a_{142} = 2+\frac{142+1}{142}\)

   weil ein \(k \in \mathbb{N}\) existiert, so dass

     \(n = 3k+1\)

   ist (nämlich \(k = 47\)).