Bestimmen Sie die partiellen Ableitungen..

Question

Aufgabe:

Text erkannt:

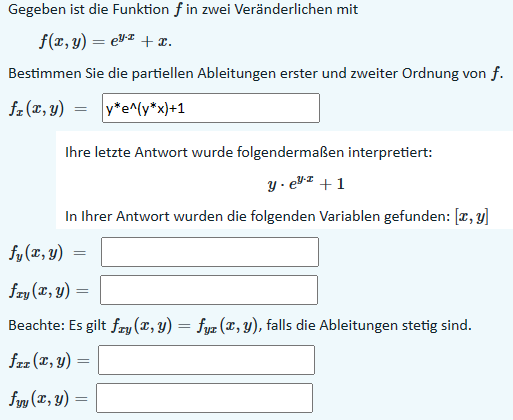
Gegeben ist die Funktion \( f \) in zwei Veränderlichen mit
\( f(x, y)=e^{y \cdot x}+x . \)
Bestimmen Sie die partiellen Ableitungen erster und zweiter Ordnung von \( f \).
\( f_{x}(x, y)=\mathrm{y}^{*} \mathrm{e}^{\wedge}\left(\mathrm{y}^{*} \mathrm{x}\right)+1 \)
Ihre letzte Antwort wurde folgendermaßen interpretiert:
\( y \cdot e^{y \cdot x}+1 \)
In Ihrer Antwort wurden die folgenden Variablen gefunden: \( [x, y] \)
\( \begin{array}{c} f_{y}(x, y)= \\ f_{x y}(x, y)= \end{array} \)
Beachte: Es gilt \( f_{x y}(x, y)=f_{y x}(x, y) \), falls die Ableitungen stetig sind.
\( \begin{array}{l} f_{x x}(x, y)= \\ f_{y y}(x, y)= \end{array} \)

Problem/Ansatz:

Ich weiß nicht wie ich die restlichen Funktionen ableiten muss. Ich würde mich über die Lösung inklusive der Erklärung freuen!

Comments

Na ja, \(f_y(x,y)\) geht doch sinngemäß so, wie die Ableitung nach \(x\), nur etwas einfacher.

Answer 1

Aloha :)

Beim Bilden der partiellen Ableitungen betrachtest du fast alle Variablen als konstante Zahlen, einzige Ausnahme ist die Variable, nach der abgeleitet wird. Hier brauchst du bei allen Ableitungen die Kettenregel.

Zur Kontrolle:$$f(x;y)=e^{xy}+x$$$$f_x(x;y)=e^{xy}\cdot y+1$$$$f_y(x;y)=e^{xy}\cdot x$$$$f_{xx}(x;y)=\partial_x(f_x(x;y))=e^{xy}{\cdot y^2}$$$$f_{xy}(x;y)=f_{yx}(x;y)=\partial_x(f_y(x;y))=e^{xy}\cdot xy+e^{xy}=e^{xy}(xy+1)$$$$f_{yy}(x;y)=\partial_y(f_y(x;y))=e^{xy}\cdot x^2$$