Bestimmen Sie den maximalen Definitionsbereich D von f.

Question

Aufgabe:

Gegeben ist die Funktion f in zwei Veränderlichen mit

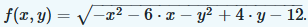
Text erkannt:

\( f(x, y)=\sqrt{-x^{2}-6 \cdot x-y^{2}+4 \cdot y-12} \)

1. Bestimmen Sie den maximalen Definitionsbereich D von f.

Text erkannt:

\( \mathbb{D}=\left\{(x, y) \in \mathbb{R}^{2} \mid\right. \)
(Nicht beantwortet) \( \neq\} \)

Geben Sie den Mittelpunkt und den Radius der Kreisscheibe an, der den maximalen Definitionsbereich D von f darstellt.

2. Kreis Mittelpunkt: M=(    |    ) 
  Radius: r=

3. Welche Fläche gehört zu dem Definitionsbereich D?

Text erkannt:

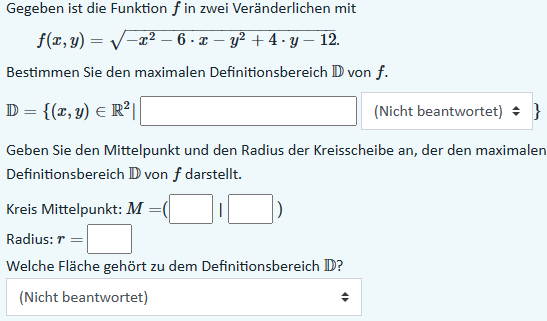
Gegeben ist die Funktion \( f \) in zwei Veränderlichen mit
\( f(x, y)=\sqrt{-x^{2}-6 \cdot x-y^{2}+4 \cdot y-12} . \)
Bestimmen Sie den maximalen Definitionsbereich \( \mathbb{D} \) von \( f \).
\( \mathbb{D}=\left\{(x, y) \in \mathbb{R}^{2} \mid\right. \)
(Nicht beantwortet) \( \neq\} \)
Geben Sie den Mittelpunkt und den Radius der Kreisscheibe an, der den maximalen Definitionsbereich \( \mathbb{D} \) von \( f \) darstellt.
Kreis Mittelpunkt: \( M=( \)
Radius: \( r= \)
Welche Fläche gehört zu dem Definitionsbereich \( \mathbb{D} \) ?
(Nicht beantwortet)

Problem/Ansatz:

Ich verstehe die Aufgabe nicht und würde mich über einen Lösungsweg und die dazugehörige Erklärung freuen!

Answer 1

\(f(x, y)=\sqrt{-x^{2}-6 \cdot x-y^{2}+4 \cdot y-12} \)

Also muss gelten \(  -x^{2}-6 \cdot x-y^{2}+4 \cdot y-12 \ge 0 \)

<=> \(  -x^{2}-6 \cdot x   -y^{2}+4 \cdot y    \ge  12   \)

<=> \(  x^{2}+6 \cdot x   +y^{2}-4 \cdot y   \le -12  \)

<=> \(  x^{2}+6 \cdot x +9   +y^{2}-4 \cdot y +4  \le -12 +13 \)

<=> \(  (x+3)^{2}    +       (y-2)^2  \le 1 \)

Ist die Kreisscheibe um (-3;2) mit r=1.

Fläche ist A=r^2 * π = π.