Sind die Ereignisse stochastisch unabhängig?

Question

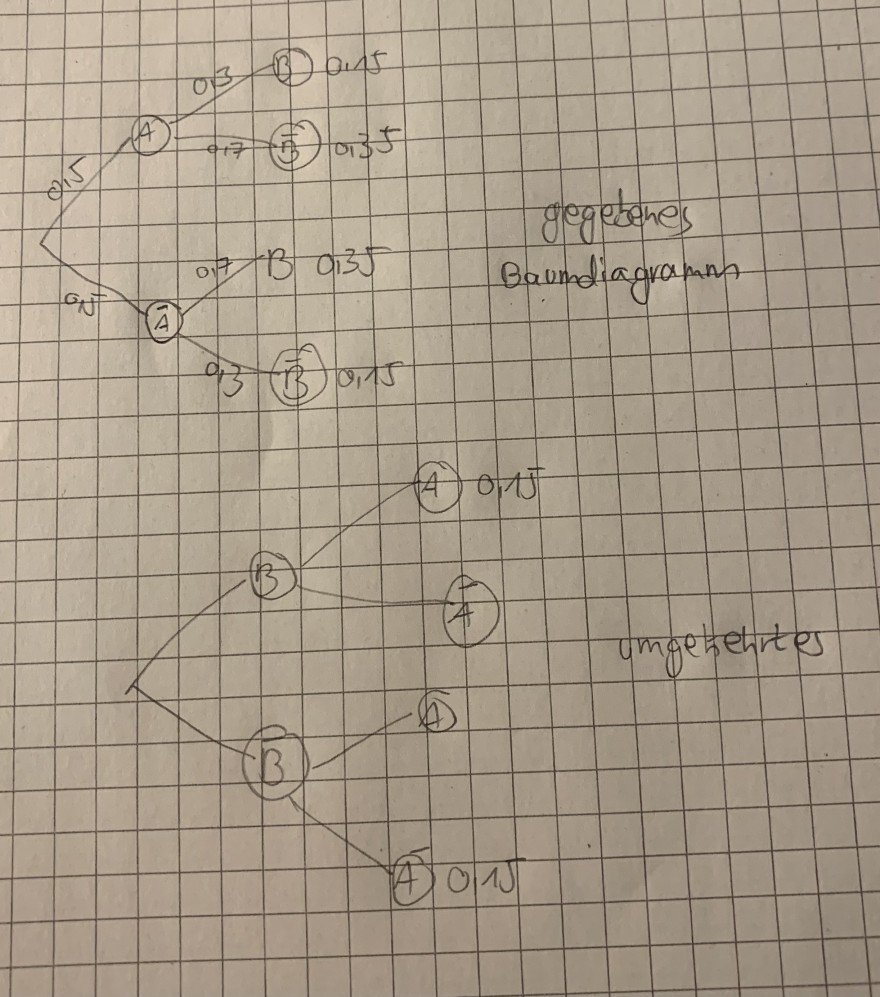
Aufgabe:

a) Fertigen Sie zu dem obigen Baumdiagramm die ein umgekehrtes an

b) Bestimmen Sie die Wahrscheinlichkeit PA(das soll kleiner als das P sein)(B (als Gegenereignis)

und beschreiben Sie, was man unter dem Ausdruck versteht.

c) Entscheiden Sie begründet, ob die Ereignisse A und B stochastisch unabhängig sind.

Problem/Ansatz:

Bei a weiß ich leider überhaupt nicht, was an die übrigen Stellen muss. Bei b sieht es leider nicht besser aus, aber für c weiß ich, dass Ereignisse unabhängig sind, wenn das Eintreten des einen Ereignisses A keinen Einfluss auf die Wahrscheinlichkeit des anderen Ereignisses B hat und umgekehrt.

Bei den Punkten, bei denen ich leider nicht weiter komme, würde ich mich sehr über Hilfe freuen.

Answer 1

Hello

a) P(A) lässt sich berechnen, über die bedingte Wahrscheinlichkeit. Nämlich P(A) =P(A geschnitten B) / P(B|A)

Sowohl ersten Dividend hast du gegeben als auch den Divisor.

den Rest kannst du dann einfach berechnen über die Gegenwahrschrinlichkeit etc.

b) die Aufgabe verstehe ich nicht von deiner Formulierung her.

C) stochastische Unabhängigkeit: P(A geschnitten B) = P(A) P(B)

Comments

\( P_{A}(\bar{B}) \)

Das ist bei b gemeint.

---

Das ist die bedingte Wahrscheinlichkeit. Die ich bei mir mit P(B|A) angegeben habe.

Diese Bedingte Wahrscheinlichkeit ist immer die Wahrscheinlichkeit am zweiten Ast deines Baumdiagramms. :)

---

Hallo, bei c) habe ich 0,3000 raus. Ist das richtig?

Und ist es richtig, dass die Ereignisse A und B stochastisch abhängig sind? Aber warum, weiß ich nicht, könnten Sie mir da behilflich sein?

---

Also bei der c) musst du überprüfen, ob für die linke Seite der gleichung das gleiche rauskommt wie auf der rechten Seite. Also ob wenn du die Wahrscheinlichkeit der zwei Ereignisse einzeln multiplizierst, das gleiche rauskommt wie wenn du die wahrscheinlichkeit berechnest, dass A und B gilt.

Die Wahrscheinlichkeit, dass A und B gilt steht immer unter am Baumdiagram dran bei dem entsprechenden Pfad A und B. Und die einzel Wahrscheinlichkeiten für das Ereignis B hast du auch direkt im Baumdiagramm gegeben und die Einzelwahrscheinlichkeit für A solltest du ja in a) berechnen. Also hast du alles, was du brauchst, um das zu überprüfen. Wozu deine 0,3 gehört, weiß ich jetzt nicht

---

Ok, vielen lieben Dank. Wie ich bei c vorgehen kann, habe ich verstanden. Könnten Sie eventuell einmal nachschauen, ob ich das umgekehrte Baumdiagramm überhaupt richtig ausgefüllt habe, und wenn nein, mir erklären, was ich falsch gemacht habe. Das würde mich sehr freuen, weil das die einzige Aufgabe ist, bei der ich noch Probleme habe.

Text erkannt:

(A) 0,15
0,7
(A) \( 0,3 I \)
(A) 0,35
Abbildung 2
(A) 0,15

---

Das Baumdiagramm ist korrekt :)

---

Super, vielen Dank für die Rückmeldung. Und ist dann die bedingte Wahrscheinlichkeit bei b mit 0,35 auch richtig? Viele Grüße