a) Wie wahrscheinlich ist es, dass mindestens 22 Personen aus der Stichprobe spendenfreudig sind, wenn das Verhalten der Menschen sich nicht verändert hat??
P(X ≥ 22 | n = 100 ; p = 0.2) = 0.3460
Das hast du richtig.
b) Es wird vermutet, dass die Kampange erfolgreich war. Diese Hypothese soll auf einem Signifikanzniveau von alpha= 10% getestet werden. Entwickeln Sie die Entscheidungsregel.
Suche das linksseitige Intervall in dem mind. 90% der Werte liegen.
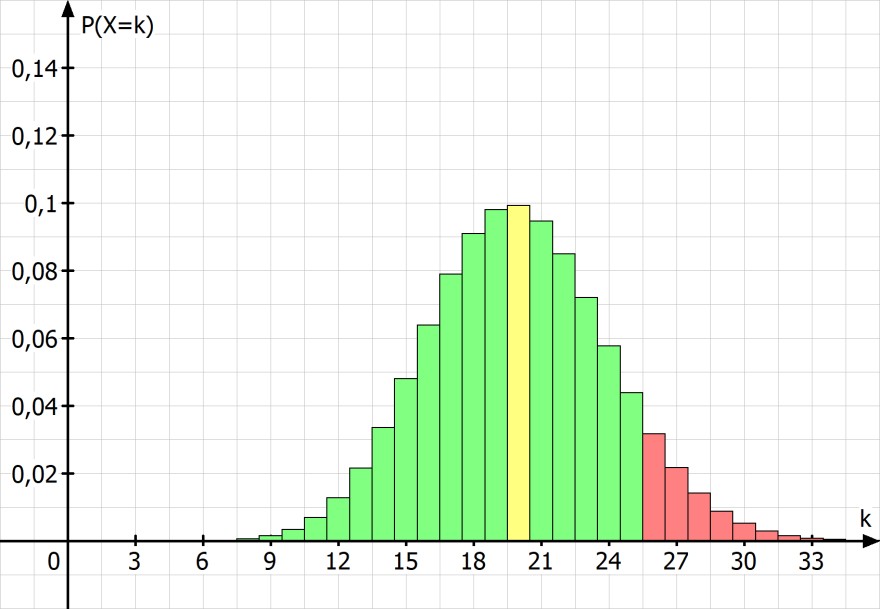
Bei höchstens 27 Spendern kann die Nullhypothese nicht abgelehnt werden. Ab 28 Spendern werden wir die Nullhypothese ablehnen.
c) DIe Entscheidungsregel soll folgendermaßen lauten: Geben weniger als 27 der 100 Befragten an, dass sie spenden wollen, so wird für H0 entschieden, andernfalls für H1. Wie groß ist der alpha-Fehler? WIe groß ist der beta-Fehler, wenn die Spendenfreudigkeit durch die Kampagne auf 30% gesteigert werden konnte??
Hier brauchst du wieder nur die Binomialverteilung wie unter a) anwenden.
α = P(X ≥ 27 | n = 100 ; p = 0.2) = ...
β = P(X < 27 | n = 100 ; p = 0.3) = ...