Mathematische Aussagen wie umformulieren?

Question

Aufgabe: Formuliere dir Aussagen rigoros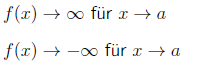

Text erkannt:

\( f(x) \rightarrow \infty \) für \( x \rightarrow a \)
\( f(x) \rightarrow-\infty \text { für } x \rightarrow a \)

Problem/Ansatz: Der Begriff "rigoros" taucht weder in meiner Vorlesung noch unserem Skript auf. Weiß jemand, was hier zu tun ist?

Answer 1

Hallo,

rein formal widersprechen sich doch die beiden Aussagen oben - oder nicht! Wie ist es denn nun, wird \(f(x)\) Minus oder Plus unendlich, wenn \(x\) gegen den Wert Wert \(a\) läuft?

Aber es kann trotzdem korrekt sein, wenn man bei dem Ausdruck \(x \to a\) noch die Seite hinzufügt, von der man sich dem Wert \(a\) nähert. Das wäre dann wohl rigoros formuliert.

Siehe dazu auch: https://www.matheretter.de/wiki/grenzwerte-rechtseitig-linksseitig

Comments

Danke für den ausführlichen Hinweis, das hilft mir schon weiter. Vermute eigentlich, dass die Aussagen jeweils gesondert zu betrachten sind, sodass unendlich und minus unendlich nicht gleichzeitig für f(x) angenommen werden sollen. Die Aufgabe ist einfach unglücklich formuliert.

---

Vieleicht sollst Du eine mathematische Definition für den Sachverhalt

$$\lim_{x \to a}f(x)=\infty$$

formulieren.