Orangendurchmesser und Erwartungswert

Question

Aufgabe:

Wie berechne ich die Abweichung vom Erwartungswert?

Die Durchmesser der Orangen einer bestimmten Sorten sind N(8cm; 2.25cm)-verteilt. Man sollte für die Lieferung von 10000 Orangen die Anzahl mit dem Durchmesser mit weniger als 1cm Abweichung vom Erwartungswert bestimmten.

Problem/Ansatz:

Kann mir wer erklären wie ich das lösen kann? Muss ich da erwartungswert + 1 und minus 1 rechnen und würde es dann so ausschauen : P(X<7 ) v P(X>9) ?

Comments

So wie ich die Aufgabe verstehe, soll man nicht "die Abweichung vom Erwartungswert berechnen".

---

Man sollte die Anzahl weniger als 1cm Abweichung vom Erwartungswert bestimmen.

---

Genau. Die Anzahl Orangen. Habe den Titel abgeändert.

\(\displaystyle n = 10000\cdot \underbrace{\frac{1}{2,25 \cdot\sqrt{2 \pi }} \cdot \int \limits_{7}^{9}  e^{\large -\frac{(x-8)^{2}}{2 \, \cdot \, 2,25^{2}}}  \, d x}_{\text{Anteil im Intervall}}\approx 3433\)

Was das bedeutet, wurde von Abakus weiter unten geschrieben. Mit der Standardnormalverteilungstabelle ginge das so:

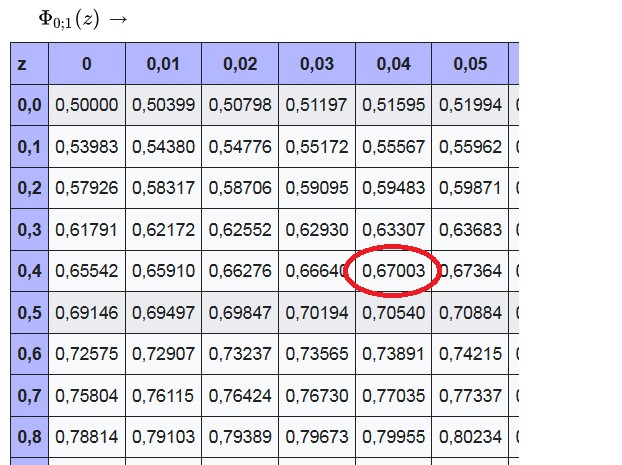
Φ(4/9) ≈ Φ(0,44) ≈ 0,67003

n ≈ 10000 * (0,67003 - (1- 0,67003)) ≈ 3401

Das ist immerhin weniger als 1 % Abweichung von der exakten Lösung.

Answer 1

Wenn die Standdardabweichung 2,25 cm sind, dann ist die vorgegebene Abweichung von 1 cm ein Bruchteil davon, nämlich 4/9 der Standardabweichung. Ermittle also zunächst  Φ(4/9).

: P(X<7 ) v P(X>9)  ist doppelt falsch, weil es um ein Intervall zwischen zwei Grenzen geht und nicht um die Teilintervalle außerhalb.