Varianz der Rendite des Portfolios

Question

Aufgabe:

Text erkannt:

\( 9.13 \).
\( \begin{array}{l} p=\alpha X+(1-\alpha) y \\ v(a x+(1-\alpha) y)=\alpha^{2} \cdot 0,2+2 \cdot \alpha \cdot(1-\alpha) \cdot(-0,2)+(1-\alpha)^{2} \cdot 0,3 \\ =0,9 \alpha^{2}-\alpha+0,3 \\ \end{array} \)

Problem/Ansatz:

Hey! Wie komme ich auf dieses Ergebnis? Und wie rechne ich danach das Minimum aus?

Comments

Es ist nachvollziehbar, dass noch keine Antwort da ist. Um was geht es? Es hilft auch nicht, dass die Aufgabe nicht besonders leserlich da steht.

Answer 1

Ich nehme an, es geht um ein Portfeuille mit zwei Finanzinstrumenten mit den Renditen X und Y mit jeweiliger Varianz V[X] = 0,2 und V[Y] = 0,3 und Kovarianz = -0,2, wobei alpha der relative Anteil von X-Instrumenten am Wert des Portfeuilles ist und beta der von Y-Instrumenten, und man will das Risiko sprich die Varianz der Portfeuilles minimieren, um herauszufinden, wo die risikoeffiziente Linie anfängt. Das alles hast Du nicht verraten; erkennen tut es darum nur, wenn man schon damit zu tun gehabt hat. Im Titel ist es zwar angedeutet. Anstatt Portfeuille kann man auch Portfolio sagen.

Eine sehr ähnliche Frage gab es schon dort allerdings ohne Kovarianz, weil dort die Renditen X und Y unabhängig waren.

Wenn nicht unabhängige Renditen, dann erweitert sich die Formel zu dem was in den einschlägigen Lehrbüchern steht:

V[P] = α^2 V[X] + 2α (1-α) Cov[X,Y] + (1-α)^2 V[Y]

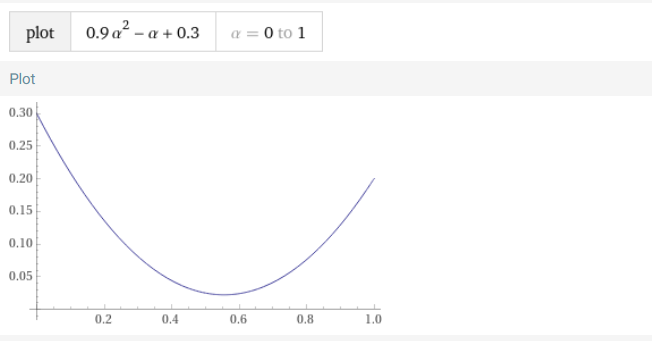
= 0,9 α^2 - α + 0,3              (Werte eingesetzt und ausmultipliziert)


Um das Minimum der Portfoliovarianz zu finden, muss man Funktion nach α ableiten und gleich null setzen:

1,8 α - 1 = 0    ⇔    α = 5 / 9


Wenig erstaunlich, hat das Portfolio darum auch eine minimale Varianz bei α = 5 / 9:

Comments

...und wenn Du noch ein bisschen mehr darüber nachdenken und lernen möchtest: Man kann sich auch überlegen, weshalb die Portfoliovarianz am linken Rand der Parabel 0,3 und am rechten Rand 0,2 beträgt.