Hallo, wisst ihr vielleicht, wie man auf die AW dieser DGL kommt, die ein Fadenpendel beschreibt? Dieser Screenshot ist von Wikipedia (https://de.wikipedia.org/wiki/Mathematisches_Pendel).
Ich verstehe die obere "anschaulichere" Herleitung und deshalb weiß ich auch, woher der -sin kommt. Aber woher kommt der Cosinus. Müsste nicht auch ein AW 0 sein, bis das Pendel ausgerenkt wird?
Text erkannt:
Bewegungsgleichung in kartesischen Koordinaten [Bearbeiten I Quelltext bearbeiten ]
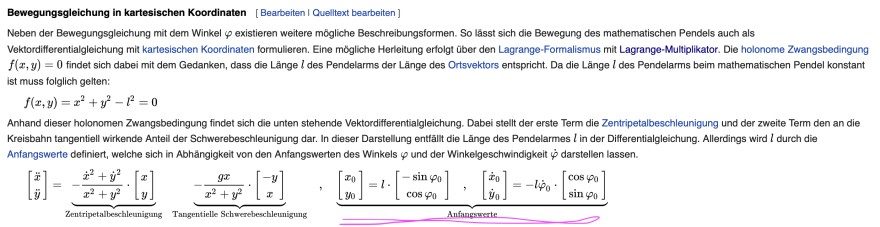
Neben der Bewegungsgleichung mit dem Winkel \( \varphi \) existieren weitere mögliche Beschreibungsformen. So lässt sich die Bewegung des mathematischen Pendels auch als Vektordifferentialgleichung mit kartesischen Koordinaten formulieren. Eine mögliche Herleitung erfolgt über den Lagrange-Formalismus mit Lagrange-Multiplikator. Die holonome Zwangsbedingung \( f(x, y)=0 \) findet sich dabei mit dem Gedanken, dass die Länge \( l \) des Pendelarms der Länge des Ortsvektors entspricht. Da die Länge \( l \) des Pendelarms beim mathematischen Pendel konstant ist muss folglich gelten:
\( f(x, y)=x^{2}+y^{2}-l^{2}=0 \)
Anhand dieser holonomen Zwangsbedingung findet sich die unten stehende Vektordifferentialgleichung. Dabei stellt der erste Term die Zentripetalbeschleunigung und der zweite Term den an die Kreisbahn tangentiell wirkende Anteil der Schwerebeschleunigung dar. In dieser Darstellung enttâllt die Länge des Pendelarmes \( l \) in der Differentialgleichung. Allerdings wird \( l \) durch die Anfangswerte definiert, welche sich in Abhängigkeit von den Anfangswerten des Winkels \( \varphi \) und der Winkelgeschwindigkeit \( \dot{\varphi} \) darstellen lassen.
\( \left[\begin{array}{c} \ddot{x} \\ \ddot{y} \end{array}\right]=\underbrace{-\frac{\dot{x}^{2}+\dot{y}^{2}}{x^{2}+y^{2}} \cdot\left[\begin{array}{l} x \\ y \end{array}\right]}_{\text {Zentripetalbeschleunigung }} \underbrace{-\frac{g x}{x^{2}+y^{2}} \cdot\left[\begin{array}{c} -y \\ x \end{array}\right]}_{\text {Tangentielle Schwereheschleunigung }}, \underbrace{\left[\begin{array}{c} x_{0} \\ y_{0} \end{array}\right]=l \cdot\left[\begin{array}{c} -\sin \varphi_{0} \\ \cos \varphi_{0} \end{array}\right],\left[\begin{array}{c} \dot{x}_{0} \\ \dot{y}_{0} \end{array}\right]=-l \dot{\varphi}_{0} \cdot\left[\begin{array}{l} \cos \varphi_{0} \\ \sin \varphi_{0} \end{array}\right]}_{\text {Anfangsarerte }} \)
Ich würde mich sehr über eure Hilfe freuen!
LG