Wie kommt man von arctans(h/5) - arctans(h/10) = 15 auf (5h)/(h^2+50) =tans(15)

Question

Die Gleichung: arctans(h/5) - arctans(h/10) = 15
soll nach h umgestellt werden:

(5h/50) = tans(15)                //Ich weiß man könnte es noch kürzen...

laut lösungsbuch: (5h)/(h²+50) =tans(15)

meine frage: wie kommt man auf die h2?
 

Comments

Steht bei euch tans und arctans für etwas Spezielles?

tan und arctan sind die üblichen Abkürzungen für Tangens und Arcustangens.

Answer 1

Du kannst nur auf beiden Seiten der Gleichung den arctan wegbringen indem du beidseits tan nimmst, wenn du auf einer Seite einen arctan isoliert dastehen hast. Benutze dazu die Additionstheoreme.

Hier jenes für arctanx - arctany

https://de.wikipedia.org/wiki/Additionstheoreme_(Trigonometrie)#Additionstheoreme

arctan(h/5) - arctan(h/10) = 15

Und jetzt die empfohlene Formel. Bruch vereinfachen…

Dann kommst du vermutlich auf die Formel in deinem Lösungsbuch.

Answer 2

Interessante Aufgabe. Mir so auch noch nicht untergekommen.
(Und ich hoffe mal tan=tans=tangens )

 

Nehmen wir der Einfachhalber h/5=x und h/10=y

Dann folgende Substitution: x=tan(a) und y=tan(b)

 

(Formelsammlung:)

tan(a-b)=(tan(a)-tan(b))/(1+tan(a)tan(b))=(x-y)/(1+xy)

 

Arctan anwenden:

a-b=arctan((x-y)/(1+xy))

Resubstitution:

arctan(x)-arctan(y)=arctan((x-y)/(1+xy))

 

Nun kümmern wir uns mal nur noch  um das Argument.

(x-y)/(1+xy)

 

Auch hier Resubstituieren wir:

 

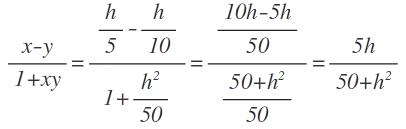
Wir haben ja den arctan und haben gerade nur das Argument angeschaut. Nun den tan nehmen und das Argument steht alleine da. Auf der rechten Seite kommt dann das tan(15) zu Stande.

 

Verstanden?
Grüße