Aufgabe:
Man soll die Eigenwerte einer Matrix berechnen
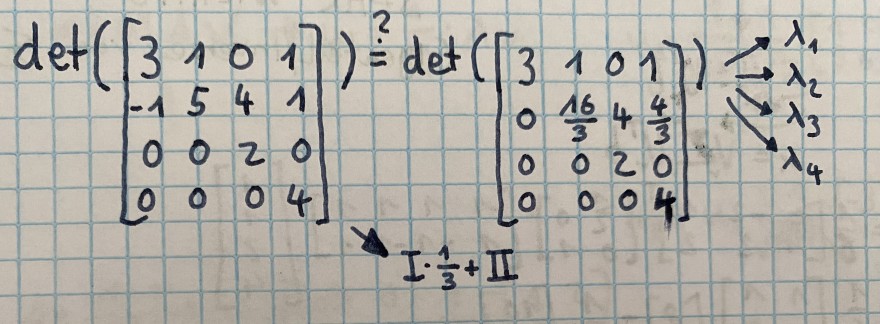
Text erkannt:
\( \operatorname{det}\left(\left[\begin{array}{cccc}3 & 1 & 0 & 1 \\ -1 & 5 & 4 & 1 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 4\end{array}\right] \stackrel{?}{\doteq}^{\operatorname{det}} \operatorname{det}\left(\left[\begin{array}{cccc}3 & 1 & 0 & 1 \\ 0 & \frac{16}{3} & 4 & \frac{4}{3} \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 4\end{array}\right]\right) \underset{\substack{\lambda_{1} \\ \overrightarrow{\lambda_{2}} \\ \lambda_{2} \\ \lambda_{3} \\ \lambda_{4}}}{ }\right. \)
Problem/Ansatz:
Normalerweise ist es doch kein Problem wenn ich die 1. Zeile mit der 2. addiere um in eine Zeilenstufenform zu kommen. Allerdings erhalte ich dann die falschen Eigenwerte. Eigentlich sollten diese nämlich 2, 4, 4, 4 lauten, wie man aber an der Diagonale meiner Umformung erkennen kann stimmen diese dann nicht überein. Wo liegt hier der Fehler?