Aloha :)
Der links- und der rechtsseitige Grenzwert des Differenzenquotienten müssen gleich sein.
Bestimmung des rechtsseitigen Grenzwertes
$$f'_+(x)=\lim\limits_{x\searrow0}\frac{f(x)-f(0)}{x-0}=\lim\limits_{x\searrow0}\frac{\cos(2x)\sin(x)-0}{x}$$Zur bestimmung des Grenzwertes betrachten wir den Einheitskeis:
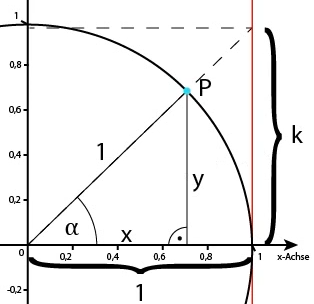
Dort erkennen wir die Strecke \(y=\sin(\alpha)\), die Länge \(\alpha\) des Kreisbogens vom Punkt \((1;0)\) bis zum Punkt \(P\) und die Strecke \(k=\tan(\alpha)\). Im ersten Quadranten, also für \(\alpha\in[0;\frac\pi2)\) gilt offensichtlich:$$y\le\alpha\le k\implies\sin(\alpha)\le\alpha\le\tan(\alpha)=\frac{\sin(\alpha)}{\cos\alpha}\implies1\le\frac{\alpha}{\sin(\alpha)}\le\frac{1}{\cos(\alpha)}$$Daher gilt für den Grenzwert \(\alpha\to0\):$$1\le\lim\limits_{\alpha\to0}\frac{\alpha}{\sin(\alpha)}\le\lim\limits_{\alpha\to0}\frac{1}{\cos(\alpha)}=1\implies\lim\limits_{\alpha\to0}\frac{\alpha}{\sin(\alpha)}=1$$
Damit gehen wir zurück zu unserem Differenzenquotienten;$$f'_+(x)=\lim\limits_{x\searrow0}\cos(2x)\cdot\lim\limits_{x\searrow0}\frac{x}{\sin(x)}=1\cdot1=1$$
Bestimmung des linksseitigen Grenzwertes
$$f'_-(x)=\lim\limits_{x\nearrow0}\frac{f(x)-f(0)}{x-0}=\lim\limits_{x\nearrow0}\frac{(ax+b)-0}{x}=\lim\limits_{x\nearrow0}\left(a+\frac{b}{x}\right)=a\quad\text{für }b=0$$Der Grenzwert existiert nur für \(b=0\) und hat dann den Wert \(a\), der für die Differenzierbarkeit im Punkt \(x_0=0\) ja gleich \(1\) sein muss.
Ergebnis
Die Funktion ist also differenzierbar für \(a=1\) und \(b=0\).