Ich dachte, man hätte vielleicht *(x+4) und *(x+3) gerechnet, aber müsste der Bruch dann nicht gekürzt werden, wenn …

Question

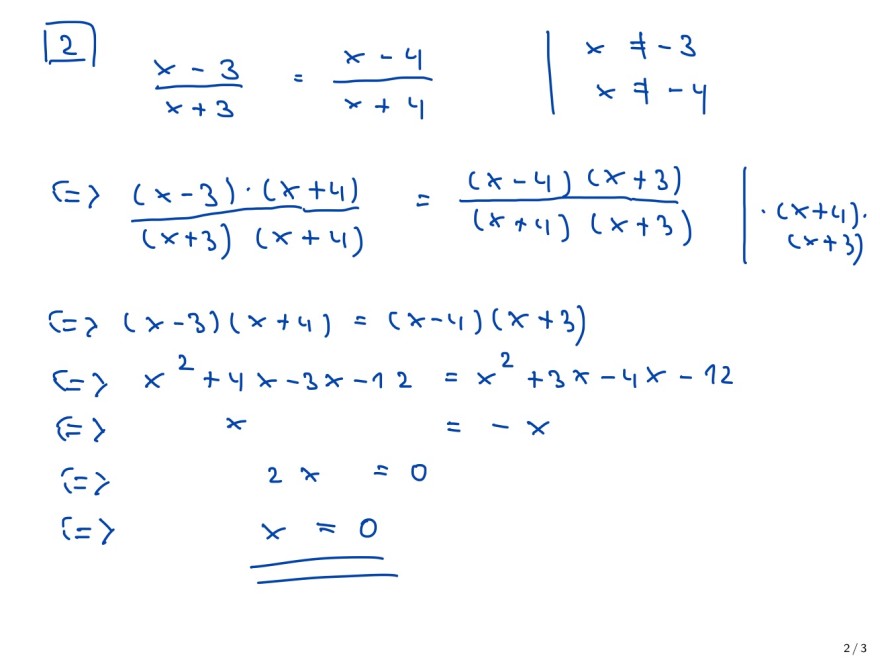
Text erkannt:

\( \Leftrightarrow \frac{x-3}{x+3}=\frac{x-4}{x+4} \mid \begin{array}{c}x \neq-3 \\ x \neq-4\end{array} \)
\( \Leftrightarrow \frac{(x-3) \cdot(x+4)}{(x+3)(x+4)}=\frac{(x-4)(x+3)}{(x+4)(x+3)} \mid \begin{array}{c}(x+4) . \\ (x+3)\end{array} \)
\( \Leftrightarrow(x-3)(x+4)=(x-4)(x+3) \)
\( \Leftrightarrow x^{2}+4 x-3 x-12=x^{2}+3 x-4 x-12 \)
\( \Leftrightarrow \quad x \quad-x \)
\( \Leftrightarrow \quad x=0 \)
\( \Leftrightarrow \quad x=0 \)

Hallo!

Meine Frage wäre, was man in der ersten Zeile gerechnet hat, um auf die zweite zu kommen. Ich dachte, man hätte vielleicht *(x+4) und *(x+3) gerechnet, aber müsste der Bruch dann nicht gekürzt werden, wenn man mit dem multipliziert, was im Nenner steht?

Und wie kommt man auf 2x = 0?

Answer 1

Hallo ,

wenn man alles auf einen Nenner gebracht hat, wird der Nenner vernachläßigt.

x² +4x-3x -12 = x² +3x-4x -12  | -x² ; +12 

                 x    = - x                     |+x

                  2x =  0      ,damit ist x= 0

Answer 2

Über Kreuz multiplizieren:

(x-3)(x+4) = (x-4)(x+3)

x^2+x-12 = x^2-x-12

x = -x

2x= 0

x=0

Answer 3

Damit wenigstens einer auf deine konkrete Frage antwortet:

Man hat den linken Bruch mit (x+4) erweitert, und man hat den rechten Bruch mit (x+3) erweitert.