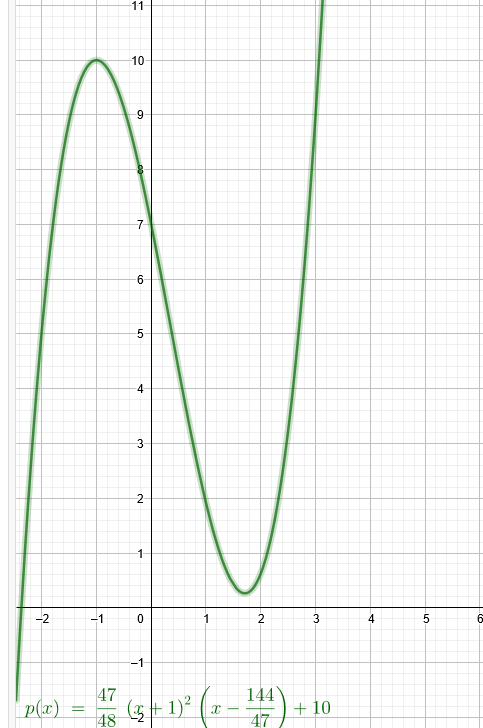
Weg über die Nullstellenform der kubischen Parabel:(gibt angenähert den gegebenen Graphen)
Ich verschiebe den Graphen um 10 Einheiten nach unten :
Maximum bei M(-1|0) , P´(3|-1) und Q´(0|-3)
f(x)=a*(x+1)^2*(x-N)
f(3)=a*(3+1)^2*(3-N)=16a*(3-N)
1.)16a*(3-N)=-1→ 1.) 16a*(N-3)=1
f(0)=a*(0+1)^2*(0-N)=a*(-N)
2.)a*(-N)=-3→2.)a*N=3 →a=\( \frac{3}{N} \) in 1.) 16*\( \frac{3}{N} \) *(N-3)=1
N=\( \frac{144}{47} \) a=\( \frac{47*3}{144} \)=\( \frac{47}{48} \)
f(x)=\( \frac{47}{48} \)*(x+1)^2*(x-\( \frac{144}{47} \) )
Nun wieder 10 Einheiten nach oben:
p(x)=\( \frac{47}{48} \)*(x+1)^2*(x-\( \frac{144}{47} \) )+10