Question

Bestimmen Sie die Gleichung einer ganzrationalen Funktion dritten grades, deren Graph punktsymmetrisch zum Ursprung ist und in H(3/54) einen HP hat. (Mit Matrix im Taschenrechner) Sehe meinen Fehler nicht.

f (3) = 54 
f ' (3) = 0 
f (-3) = -54
f ' (-3) = 0 

Ein kompletter Lösungsweg wäre sehr hilfreich, !

( es müsste -x^3+27x rauskommen)

Comments

Sehe meinen Fehler nicht.

Ich auch nicht. Bis jetzt ist alles richtig.

---

Bis dahin ja, komme aber nicht weiter bzw. das was ich gemacht habe (in funktion einsetzen) ist irgendwie falsch.

---

Wie sieht das Geichungssystem aus, dass du bekommen hast?

---

\(f(x)=ax^3+bx\\f'(x)=3ax^2\)

f (3) = 54 \(\Rightarrow 27a+3b=54\)
f ' (3) = 0\(\Rightarrow 27 a + b = 0\)

---

1: f(3) = 27a+3c = 54

2: f ' (3) = 27a+c =0

3: f (-3) = -27a-3c = -54

4: f ' (-3) = -27a +c = 0

---

Du hast in 4) einen Vorzeichenfehler.

---

Dann hast du etwas falsch in den Taschenrechner eingegeben. Aber bei zwei Gleichungen würde ich es auch mal ganz altmodisch mit dem Einsetzungsverfahren probieren.

---

Du hast in 4) einen Vorzeichenfehler

welchen denn?

---

Rechne nach! Da es ja nur um ±27 a und  ±c gehen kann und ich dir geschrieben haben, dass du dabei einen (und ich präzisiere: GENAU EINEN) Vorzeichenfehler hat, ist die Auswahl, WAS genau falsch sein könnte, nicht mehr so groß.

Schau selbstkritisch deine Rechnung an!

---

es ist immer noch falsch

---

es ist immer noch falsch

Du hast vermutlich versucht, ohne nachzudenken etwas in den TR einzugeben. Klären wir doch erst einmal ein grundlegendes Problem: Wie müsste deine vierte Gleichung richtig heißen?

---

f ' (-3) = -27a - c = 0  ?

---

Ja. Und wenn du deine dritte Gleichung mit -1 multiplizierst, erhältst du die erste.

Und wenn du deine jetzt richtige vierte Gleichung mit -1 multiplizierst, erhältst du die zweite.

Du hast also in Wirklichkkeit gar kein Gleichungssystem aus 4 Gleichungen, sondern nur aus zwei Gleichungen, die nur noch einmal wiederholt werden. Löse also nur das System aus den ersten beiden Gleichungen mit den beiden darin vorhandenen Unbekannten.

Answer 1

Aloha :)

Ein Polynomfunktion ist punktsymmetrisch, wenn die \(x\) nur ungerade Exponenten haben. Daher wählen wir als Ansatz:$$f(x)=ax^3+bx$$$$f'(x)=3ax^2+b$$Aus den beiden Angaben erhalten wir 2 Gleichungen:$$54=f(3)=a\cdot3^3+b\cdot3=27a+3b\quad\Leftrightarrow\quad18=9a+b$$$$0=f'(3)=3a\cdot3^2+b=27a+b\quad\Leftrightarrow\quad0=27a+b$$Aus der zweiten Gleichung folgt \(b=-27a\), was wir in die erste Gleichung einsetzen:$$18=9a+b=9a-27a=-18a\quad\Leftrightarrow\quad a=-1$$Aus der zweiten Gleichung folgt dann:$$b=-27a=-27\cdot(-1)=27$$Wir erhalten als Lösung:$$\boxed{f(x)=-x^3+27x}$$

~plot~ -x^3+27x ; {3|54}; {-3|-54} ; [[-4|4|-60|60]] ~plot~

Answer 2

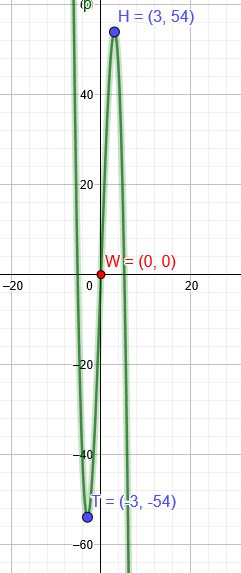
"Bestimmen Sie die Gleichung einer ganzrationalen Funktion dritten Grades, deren Graph punktsymmetrisch zum Ursprung ist und in \(H(3|54)\) einen HP hat. "

Punktsymmetrisch zum Ursprung bedeutet, dass der Tiefpunkt bei  \( T(-3|-54)\) liegt.

Ich verschiebe \(f(x)\) um 54 Einheiten nach unten:

\(H(3|54)\)→\(H´(3|0)\) doppelte Nullstelle   ;  \( T(-3|-108)\) und \(W(0|-54)\)

\(f(x)=a*(x-3)^2*(x-N)\)

\( T(-3|-108)\)

\(f(-3)=a*(-3-3)^2*(-3-N)=36a*(-3-N)\)

\(36a*(-3-N)=-108\)   →  \(a*(3+N)=3\)   →

1.)   \(a=\frac{3}{3+N}\)

\(f(x)=\frac{3}{3+N}*(x-3)^2*(x-N)\)

\(W(0|-54)\)

\(f(0)=\frac{3}{3+N}*(0-3)^2*(0-N)=-54\)         \(\frac{1}{3+N}*N=2\)        \(N=-6\)  ∈  1.)  \(a=\frac{3}{3-6}=-1\)

\(f(x)=-(x-3)^2*(x+6)\)

\(p(x)=-(x-3)^2*(x+6)+54\)