Question

Bestimmen Sie die Gleichung einer ganzrationalen Funktion dritten grades, deren Graph punktsymmetrisch zum Ursprung ist und in H(3/54) einen HP hat. (Mit Matrix im Taschenrechner) Sehe meinen Fehler nicht.

f (3) = 54 
f ' (3) = 0 
f (-3) = -54
f ' (-3) = 0 

Ein kompletter Lösungsweg wäre sehr hilfreich, !

( es müsste -x³+27x rauskommen)

Comments

Sehe meinen Fehler nicht.

Ich auch nicht. Bis jetzt ist alles richtig.

---

Bis dahin ja, komme aber nicht weiter bzw. das was ich gemacht habe (in funktion einsetzen) ist irgendwie falsch.

---

Wie sieht das Geichungssystem aus, dass du bekommen hast?

---

$f(x)=ax^3+bx\\f'(x)=3ax^2$

f (3) = 54 $\Rightarrow 27a+3b=54$
f ' (3) = 0$\Rightarrow 27 a + b = 0$

---

1: f(3) = 27a+3c = 54

2: f ' (3) = 27a+c =0

3: f (-3) = -27a-3c = -54

4: f ' (-3) = -27a +c = 0

---

Du hast in 4) einen Vorzeichenfehler.

---

Dann hast du etwas falsch in den Taschenrechner eingegeben. Aber bei zwei Gleichungen würde ich es auch mal ganz altmodisch mit dem Einsetzungsverfahren probieren.

---

Du hast in 4) einen Vorzeichenfehler

welchen denn?

---

Rechne nach! Da es ja nur um ±27 a und  ±c gehen kann und ich dir geschrieben haben, dass du dabei einen (und ich präzisiere: GENAU EINEN) Vorzeichenfehler hat, ist die Auswahl, WAS genau falsch sein könnte, nicht mehr so groß.

Schau selbstkritisch deine Rechnung an!

---

es ist immer noch falsch

---

es ist immer noch falsch

Du hast vermutlich versucht, ohne nachzudenken etwas in den TR einzugeben. Klären wir doch erst einmal ein grundlegendes Problem: Wie müsste deine vierte Gleichung richtig heißen?

---

f ' (-3) = -27a - c = 0  ?

---

Ja. Und wenn du deine dritte Gleichung mit -1 multiplizierst, erhältst du die erste.

Und wenn du deine jetzt richtige vierte Gleichung mit -1 multiplizierst, erhältst du die zweite.

Du hast also in Wirklichkkeit gar kein Gleichungssystem aus 4 Gleichungen, sondern nur aus zwei Gleichungen, die nur noch einmal wiederholt werden. Löse also nur das System aus den ersten beiden Gleichungen mit den beiden darin vorhandenen Unbekannten.

Answer 1

Aloha :)

Ein Polynomfunktion ist punktsymmetrisch, wenn die $x$ nur ungerade Exponenten haben. Daher wählen wir als Ansatz:$$f(x)=ax^3+bx$$$$f'(x)=3ax^2+b$$Aus den beiden Angaben erhalten wir 2 Gleichungen:$$54=f(3)=a\cdot3^3+b\cdot3=27a+3b\quad\Leftrightarrow\quad18=9a+b$$$$0=f'(3)=3a\cdot3^2+b=27a+b\quad\Leftrightarrow\quad0=27a+b$$Aus der zweiten Gleichung folgt $b=-27a$, was wir in die erste Gleichung einsetzen:$$18=9a+b=9a-27a=-18a\quad\Leftrightarrow\quad a=-1$$Aus der zweiten Gleichung folgt dann:$$b=-27a=-27\cdot(-1)=27$$Wir erhalten als Lösung:$$\boxed{f(x)=-x^3+27x}$$

Plotlux öffnen

f₁(x) = -x³+27xP(3|54)P(-3|-54)Zoom: x(-4…4) y(-60…60)

Answer 2

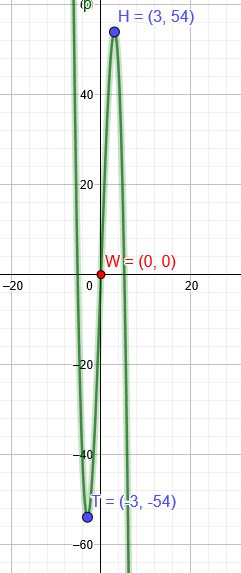
"Bestimmen Sie die Gleichung einer ganzrationalen Funktion dritten Grades, deren Graph punktsymmetrisch zum Ursprung ist und in $H(3|54)$ einen HP hat. "

Punktsymmetrisch zum Ursprung bedeutet, dass der Tiefpunkt bei  $T(-3|-54)$ liegt.

Ich verschiebe $f(x)$ um 54 Einheiten nach unten:

$H(3|54)$→$H´(3|0)$ doppelte Nullstelle   ;  $T(-3|-108)$ und $W(0|-54)$

$f(x)=a*(x-3)^2*(x-N)$

$T(-3|-108)$

$f(-3)=a*(-3-3)^2*(-3-N)=36a*(-3-N)$

$36a*(-3-N)=-108$   →  $a*(3+N)=3$   →

1.)   $a=\frac{3}{3+N}$

$f(x)=\frac{3}{3+N}*(x-3)^2*(x-N)$

$W(0|-54)$

$f(0)=\frac{3}{3+N}*(0-3)^2*(0-N)=-54$         $\frac{1}{3+N}*N=2$        $N=-6$  ∈  1.)  $a=\frac{3}{3-6}=-1$

$f(x)=-(x-3)^2*(x+6)$

$p(x)=-(x-3)^2*(x+6)+54$