Pyramide Vektor Aufgabe Hilfe

Question

Aufgabe:

Gegeben ist das gleichschenklige Dreieck ABC mit A (2/6/0), B (0/5/2) und C (3/1,5/1) sowie der Spitze S, die sich auf der Gerade h:x = \( \begin{pmatrix} 3\\1,5\\1 \end{pmatrix} \) + t × \( \begin{pmatrix} 1\\0\\1\end{pmatrix} \) bewegt. Die Spitze ist folglich der Punkt (t+3/1,5/t+1).

a) Geben Sie im Sachzusammenhang eine Frage an, die keinen Winkel beinhaltet und die mit folgender Gleichung gelöst wird (siehe Bild).

b) Eine Ebene F teilt die Pyramide in zwei gleich große Volumina. Wie kann man eine Gleichung für F erhalten?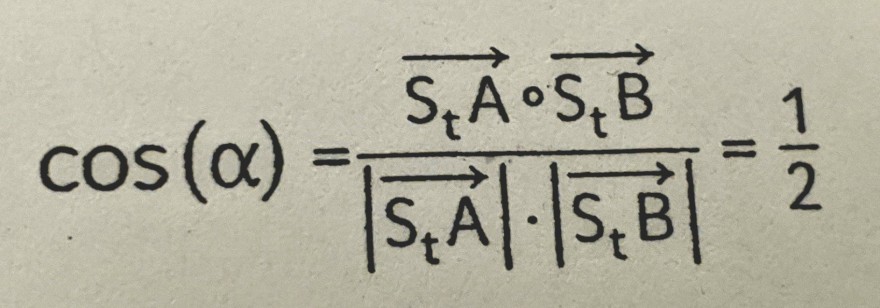

Text erkannt:

\( \cos (\alpha)=\frac{\overrightarrow{S_{t} A} \cdot \overrightarrow{S_{t} B}}{\left|\overrightarrow{S_{t} A}\right| \cdot\left|\overrightarrow{S_{t} B}\right|}=\frac{1}{2} \)

Problem/Ansatz:

Könnt ihr mir helfen? Ich komme nicht weiter..

Answer 1

Hallo,

da cos60°=½ gilt, ist das Dreieck ∆ABS dann sogar gleichseitig.

Also: Für welchen Wert von t ist ∆ABS gleichseitig?

Bzw. nach dem Hinweis von hj2166:

"Für welche Werte von t könnte das Dreieck ABS gleichseitig sein ?"

Comments

Wenn Der Winkel ∠ASB = 60° beträgt (was übrigens nie vorkommt), muss doch das Dreieck ΔASB noch lange nicht gleichseitig sein solange man seine Gleichschenkligkeit (die allerdings für jedes t vorliegt) nicht nachgewiesen hat.

---

da cos60°=½ gilt, ist das Dreieck ∆ABS dann sogar gleichseitig.

Es geht um das Dreieck ABC.

---

@hj2166

Meine Antwort bezieht sich auf Aufgabe a), zu der eine Frage gefunden werden und kein Nachweis geführt werden soll.

@abakus

Nein, es geht um ∆ABS.

:-)

---

Mein Kommentar läuft doch darauf hinaus, dass du die Frage "Für welche Werte von t könnte das Dreieck ABS gleichseitig sein ?" hättest formulieren sollen.

---

Ach so. Da ich die Aufgabe nicht durchgerechnet habe, wusste ich nicht, ob die Aufgabe lösbar ist.

---

Da Bild zur Aufgabe: \(\triangle ABC\) ist das grüne Dreieck.

Das rote Dreieck wäre ein gleichseitiges,dessen eine Seite \(=AB\) ist.

---

ob die Aufgabe lösbar ist.

Darum geht es mir auch nicht, sondern um die Logik.

Hier erfüllen zwei Punkte S auf der Geraden h die Winkelbedingung, aber es ergibt sich kein gleichseitiges Dreieck. Die von dir gestellte Frage kann also im Allgemeinen nur durch Betrachten der vorgelegten Gleichung nicht beantwortet werden.