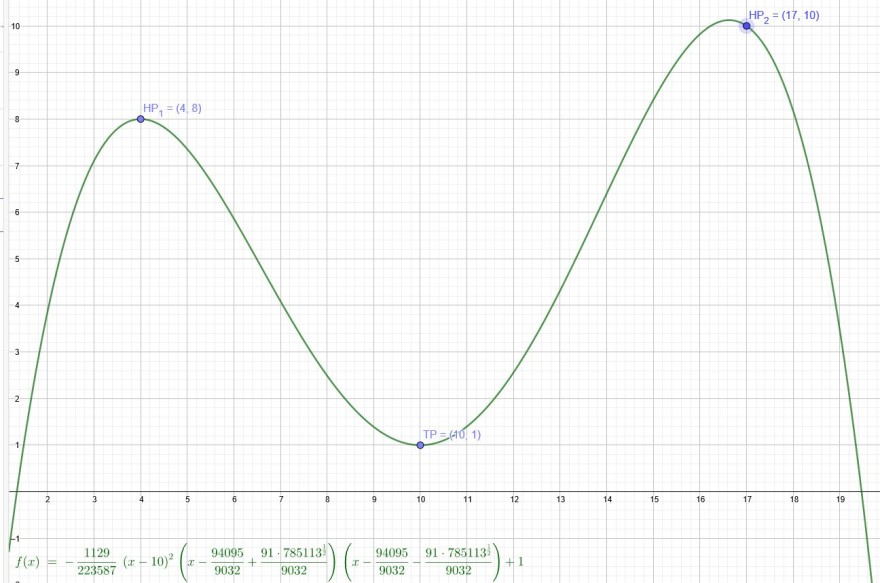
Ich verschiebe den Graphen von f(x) um 1 Einheit nach unten:
HP 1: (4|8)→HP´ 1: (4|7)
HP 2: (17|10)→HP´ 2: (17|9)
TP: (10|1)→TP´: (10|0) doppelte Nullstelle
\(f(x)=a*(x-10)^2*(x-N_1)*(x-N_2)\)
HP´ 1: (4|7):
\(f(4)=a*(4-10)^2*(4-N_1)*(4-N_2)\) → \(36a*(4-N_1)*(4-N_2)=7\)
HP´ 2: (17|9)
\(f(17)=a*(17-10)^2*(17-N_1)*(17-N_2)\) →\(49a*(17-N_1)*(17-N_2)=9\)
HP´1: (4|7) waagerechte Tangente:
\(f´(x)=a*[(2x-20)*(x-N_1)*(x-N_2)+(x-10)^2*(x-N_2)+(x-10)^2*(x-N_1)]\)
\(f´(4)=a*[(2*4-20)*(4-N_1)*(4-N_2)+(4-10)^2*(4-N_2)+(4-10)^2*(4-N_1)]\)
\(a*[(-12)*(4-N_1)*(4-N_2)+36*(4-N_2)+36*(4-N_1)]=0\)
p(x), a , N_1 und N_2 sind aus der Zeichnung ablesbar. In der Zeichnung muss es statt f(x) p(x) heißen.
Der 2. HP ist knapp daneben.