Question

Wie kommt es zu dieser Ableitung nach y?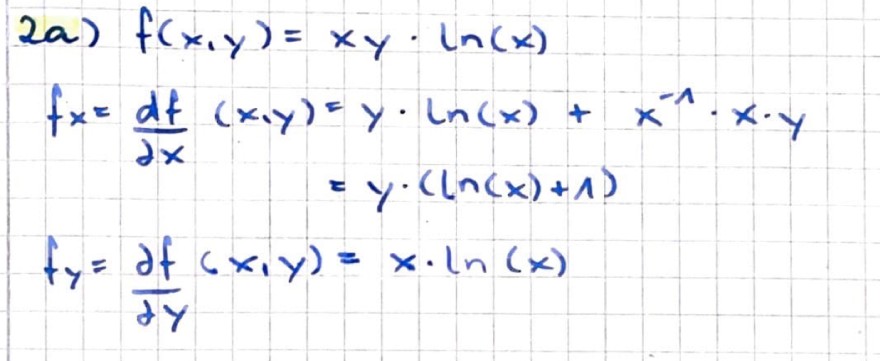

Text erkannt:

2a) \( \begin{aligned} f(x, y) & =x y \cdot \ln (x) \\ f_{x}=\frac{d f}{\partial x}(x, y) & =y \cdot \ln (x)+x^{-1} \cdot x \cdot y \\ & =y \cdot(\ln (x)+1) \\ f_{y}=\frac{\partial f}{\partial y}(x, y) & =x \cdot \ln (x)\end{aligned} \)

Answer 1

Für die Ableitung nach y kannst du x und ln(x) als konstant

betrachten.

Answer 2

Na ja, \(x\cdot\ln(x)\) ist für die partielle Ableitung dach \(\textrm{d}y\) konstant. Nach der Faktorregel bleibt es erhalten. Das \(y\) fällt weg.

Answer 3

Behandle x und lnx wie eine Zahl.