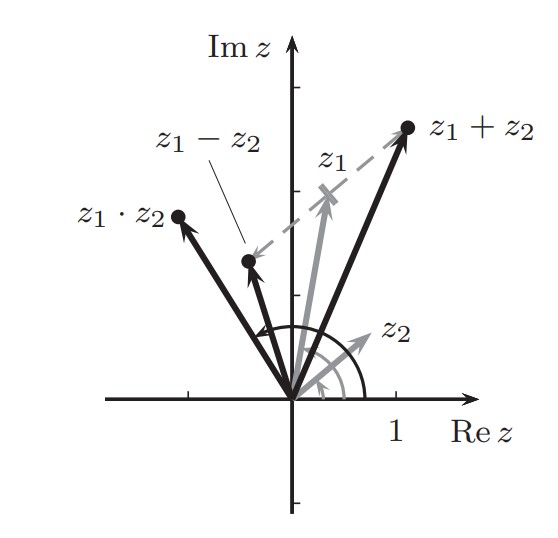
Wie kann man komplexe Zahlen grafisch multiplizieren?
"Bei der Multiplikation werden die Längen der Zeiger multipliziert und die Winkel addiert."
Das mit den Winkeln verstehe ich ja, das kann man anhand eines Geodreiecks in der Zeichnung machen. Aber wie soll das mit der Multiplikation der Zeiger klappen?
Hier kann man sehen, dass z1 und z2 gegeben sind. Aber wenn ich messe, wie lang die jeweiligen Zeiger sind und dann die zusammen multipliziere, komme ich auf eine andere Länge. Ich mein, hier ist ja z1 * z2 so lang wie allein schon z1. Also kann das hier mit der Multiplikation irgendwie nicht stimmen.