Question

Aufgabe:Was hat man bei diesem Schritt gemacht ?

Ich versteh den Ausdruck Klammere den Faktor aus dem Ausdruck aus nicht

Text erkannt:

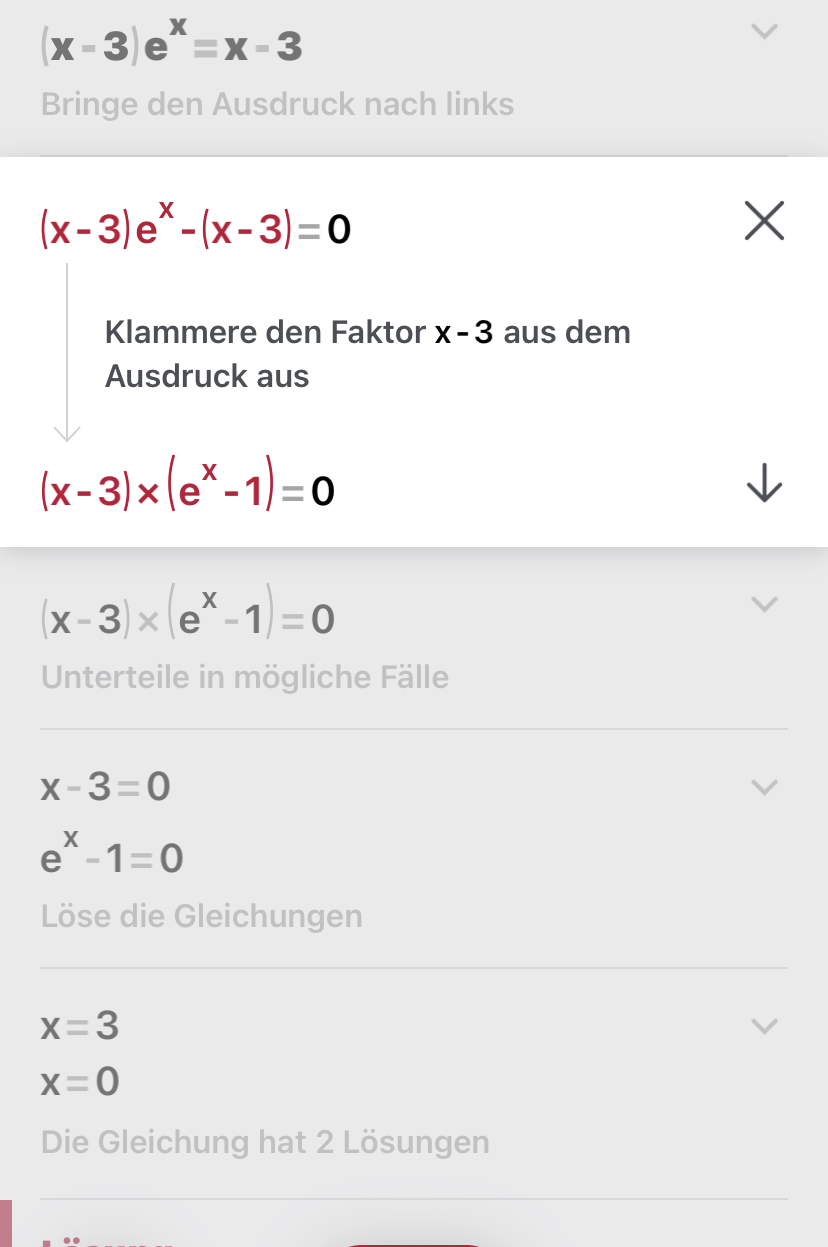
\( (x-3) e^{x}=x-3 \)
Bringe den Ausdruck nach links
\( (x-3) e^{x}-(x-3)=0 \)
Klammere den Faktor \( \mathbf{x}-\mathbf{3} \) aus dem Ausdruck aus
\( (x-3) \times\left(e^{x}-1\right)=0 \)
\( (x-3) \times\left(e^{x}-1\right)=0 \)
Unterteile in mögliche Fälle
\( \begin{array}{l} x-3=0 \\ e^{x}-1=0 \end{array} \)
Löse die Gleichungen
\( \begin{array}{l} x=3 \\ x=0 \end{array} \)
Die Gleichung hat 2 Lösungen

Answer 1

Wie es dasteht: man hat ausgeklammer

ab-ac= a(b-c)

a(b+c)-d(b+c) = (b+c)(a-d)

ausklammern = faktorisieren = Produkt erzeugen

https://www.mathebibel.de/ausklammern

Answer 2

Hallo,

\( (x-3) e^{x}-(x-3)=0 \)

\( \green{(x-3) \cdot} e^{x}-\green{(x-3)\cdot}1=0 \)

\( \green{(x-3) \cdot} (e^{x}-1)=0 \)

:-)