f(x)= 1- 6/x + 5/x2 = (x2 -6x+5) / x2
Ein Bruch ist 0, wenn der Zähler 0 ist (und der Nenner nicht 0 ist)
Nullstellen:
0= x^2 -6x + 5 |pq-Formel oder einfacher direkt faktorisieren
= (x-1)(x-5)
x1= 1, x2=5
Davon soll ich jetzt die Nullstellen berechnen und das Verhalten für x --> 0 untersuchen,
Das die Polstelle doppelt ist, gibt es an der Polstelle keinen Vorzeichenwechsel. Es gilt
lim (x->0) f(x) = + ∞
sowie Extrema,Wendepunkte und Aymptote bestimmen..
f(x)= 1- 6/x + 5/x2 = (x2 -6x+5) / x2
f(x) = 1 -6x^{-1} + 5x^{-2}
f ' (x) = 0 + 6x^{-2} - 10 x^{-3} = (6x - 10) / x^3
f ''(x) = -12x^{-3} + 30x^{-4} = (-12x + 30)/x^4
Extrema
f ' (x) = 0 + 6x^{-2} - 10 x^{-3} = (6x - 10) / x^3
f '(x) = 0
6x-10 = 0
6x = 10
x = 10/6 = 5/3
f(5/3) = -0.8
T (1.66667 , -0.8) liegt zwischen den beiden Nullstellen unterhalb der x-Achse: Daher rel. Minimum.
f ''(x) = -12x^{-3} + 30x^{-4} = (-12x + 30)/x^4
-12x + 30= 0
30= 12x
30/ 12 = x = 2.5
f(2.5) = -0.6
W(2.5, -0.6) ist der Wendepunkt.
Asymptote: Betrachte die ursprüngliche Form der Funktionsgleichung:
f(x)= 1- 6/x + 5/x2
für x gegen unendlich gehen sowohl 6/x als auch 5/x^2 gegen 0.
Die Gleichung der (horizontalen) Asymptote ist daher
g(x) = 1
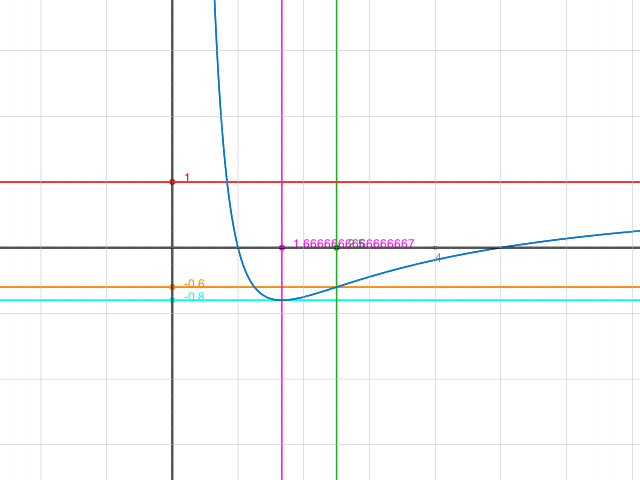
Hier noch die Skizzen zur Kontrolle:
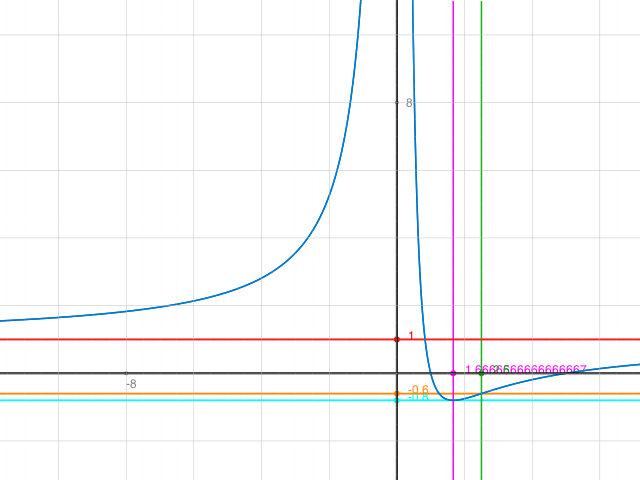
Etwas rangezoomt: