Aloha :)
zu a) Halbkreisring
Hier bietet sich die Berechnung in Polarkoordinaten an. Der Radius liegt zwischen 3cm und 5cm, also ist \(r\in[3;5]\). Der Polarwinkel muss die Halbkreise überstreichen, also ist \(\varphi\in[0;\pi]\). Damit haben wir folgende Substitution von \((x;y)\) nach \((r;\varphi)\):$$\binom{x}{y}=\binom{r\cos\varphi}{r\sin\varphi}\quad;\quad r\in[3;5]\quad;\quad\varphi\in[0;\pi]$$
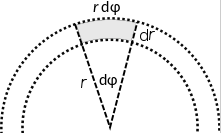
Das Flächenelement \(dA=dx\,dy\) wird durch den Übergang zu Polarkoordinaten verzerrt. Wenn sich der Radius um \(dr\) ändert und der Polarwinkel um \(d\varphi\), entsteht ein kleines Kreissegment mit der Länge \(dr\) und der Breite \(r\,d\varphi\). In infinitesimaler linearer Näherung ist daher:$$dx\,dy=dA=r\,d\varphi\,dr=r\,dr\,d\varphi$$
Damit formulieren wir das gesuchte Integral:$$I=\int\limits_A(x+y)\,dA=\int\limits_{r=3}^5\;\,\int\limits_{\varphi=0}^\pi(\underbrace{r\cos\varphi}_{=x}+\underbrace{r\sin\varphi}_{=y})\,\underbrace{r\,dr\,d\varphi}_{=dA}=\int\limits_{r=3}^5r^2\,dr\int\limits_{\varphi=0}^\pi(\cos\varphi+\sin\varphi)\,d\varphi$$$$\phantom I=\left[\frac{r^3}{3}\right]_{r=3}^5\cdot\left[\sin\varphi-\cos\varphi\right]_{\varphi=0}^\pi=\left(\frac{5^3}{3}-\frac{3^3}{3}\right)\cdot\left(1-(-1)\right)=\frac{196}{3}=65,\overline3$$
zu b) Quader
Aus der Skizze (b) lesen wir \(x\in[0;2]\) und \(y\in[0;3]\) und aus (c) folgt \(z\in[0;4]\).
Damit können wir das Integral direkt formulieren:$$I=\int\limits_V xyz^2\,dV=\int\limits_{x=0}^2\;\int\limits_{y=0}^3\;\int\limits_{z=0}^4xyz^2\,dx\,dy\,dz=\int\limits_{x=0}^2x\,dx\int\limits_{y=0}^3y\,dy\int\limits_{z=0}^4z^2\,dz$$$$\phantom I=\left[\frac{x^2}{2}\right]_0^2\cdot\left[\frac{y^2}{2}\right]_0^3\cdot\left[\frac{z^3}{3}\right]_0^4=2\cdot\frac92\cdot\frac{64}{3}=192$$