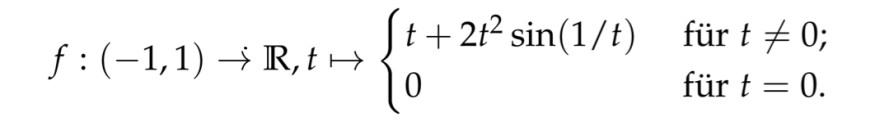Hallo zusammen,
ich habe folgende Funktion und möchte mithilfe der Folgenstetigkeit zeigen, dass f in t=0 unstetig ist.
Ich finde nur leider keine Nullfolge, die in f eingesetzt nicht gegen f(0)=0 konvergiert.
Oder muss man dies hier anders zeigen? In der selben Aufgabe habe ich gezeigt, dass f differenzierbar ist und beschränkt - hilft das etwas?
Oder ist der Trick dahinter, dass ich l´Hospital anwende beim Einsetzen einer Nullfolge? Das habe ich versucht aber komme auf keinen grünen Zweig…
Ich freue mich auf eine Antwort!