Hallo,
Bestimme einen Punkt als Orts- und zwei andere als Richtungsvektoren und dann die Parametergleichung der Ebene, z.B.
\(\overrightarrow {OA}+r\cdot \overrightarrow {AS}+s\cdot \overrightarrow {AB}\)
[spoiler]
\(\begin{pmatrix} 0\\1\\1 \end{pmatrix}+r\cdot \begin{pmatrix} -3\\3\\8 \end{pmatrix}+s\cdot \begin{pmatrix} 0\\6\\0 \end{pmatrix}\)
[/spoiler]
Volumen \(V=\frac{1}{3}G\cdot h\)
Den Flächeninhalt der dreieckigen Grundfläche kannst du mit Hilfe des Kreuzprodukts berechnen. Dabei ist der Betrag des Kreuzprodukts : 2 der Flächeninhalt des Dreiecks. Wähle dabei zwei Richtungsvektoren, die vom gleichen Punkt ausgehen.
[spoiler]
\(\vec{a}=\overrightarrow {AB}\quad \vec{b}=\overrightarrow {AC}\\ \vec{a}=\begin{pmatrix} 0\\6\\0 \end{pmatrix}\quad \vec{b}=\begin{pmatrix} -6\\6\\0 \end{pmatrix}\\ A_{Dreieck}=0,5\cdot \vec{a}\otimes \vec{b}=0,5\cdot 36=18\)
[/spoiler]
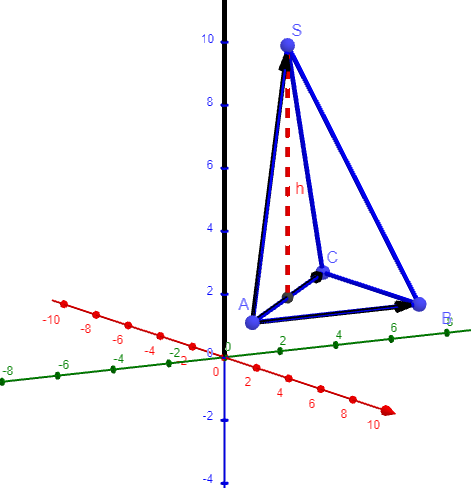
Die Höhe h ist der Abstand des Punktes S zur Grundfläche. Bei diesem Dreieck genügt es, den Abstand vom Mittelpunkt der Strecke AC zur Spitze S zu berechnen. Besser gesagt, die Länge entspricht der Differenz der z-Koordinaten von S und den Punkten A, B und C.
[spoiler]
\(V=\frac{1}{3}\cdot 18\cdot8=48 \)
[/spoiler]
Melde dich, falls du noch Fragen hast.
Gruß, Silvia