Text erkannt:
2)(8 P.) Gegeben ist die Folge \( \left(a_{n}\right)_{n \geq 0} \) mit \( a_{0}=0, a_{1}=1 \) und \( a_{n}=a_{n-1}+a_{n-2} \) für \( n \geq 2 \). Zeigen Sie mittels vollständiger Induktion, dass
\( \sum \limits_{i=0}^{n} a_{i}^{2}=a_{n} a_{n+1} . \)
Aufgabe:
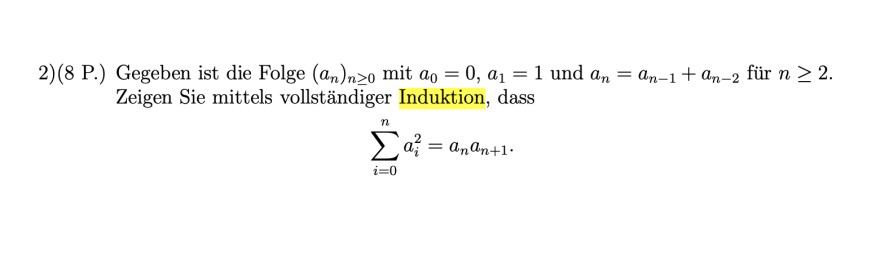
Problem/Ansatz:
Ich wollte von dem linken Teil der Induktionsbehauptung auf den rechten Teil schließen, da ich das typischerweise von Induktionsbeispielen mit Summenformel gewohnt bin. Nun geht es aber gleichzeitig auch um eine Folge, was mich etwas aus dem Konzept bringt. Nach dem Induktionsanfang und der Induktionsvoraussetzung habe ich im Induktionsschritt die ∑ von i=0 bis n+1 ai2 durch ∑ von i=0 bis n ai2 + ∑ von i=n+1 bis n + 1 gezeigt. Dabei habe ich ∑ von i=0 bis n ai2 durch den rechten Teil der oben gezeigten Gleichung ersetzt und ∑ von i=n+1 bis n + 1 als an+12 definiert. Nun sollte ∑von i=0 bis n+1 gleich an · an+1 + an+12 sein dies habe ich versucht so lange umzuformen, bis der rechte Teil der Gleichung an+1 · an+2 ergibt. Da scheitere ich allerdings, da ich die Gleichung nur bis an+1 · (an-1 + an-2 + an+1) umformen konnte und ich nicht wirklich weiß, was ich jetzt mit diesen ganzen a's anfangen soll. Die Frage ist, ob ich das Beispiel überhaupt richtig angegangen bin. Ich würde mich sehr freuen, wenn mir jemand dabei helfen könnte.