OK, dann versuche ich, dir die Schritte verständlicher nahezubringen.
Scheitelpunktform einer Parabel: \(f(x)=a(x-d)^2+e\)
Der Scheitelpunkt (niedrigster oder höchster Punkt) der Parabel hat die Koordinaten S (d | e).
Setze die Koordinaten in die Gleichung ein.
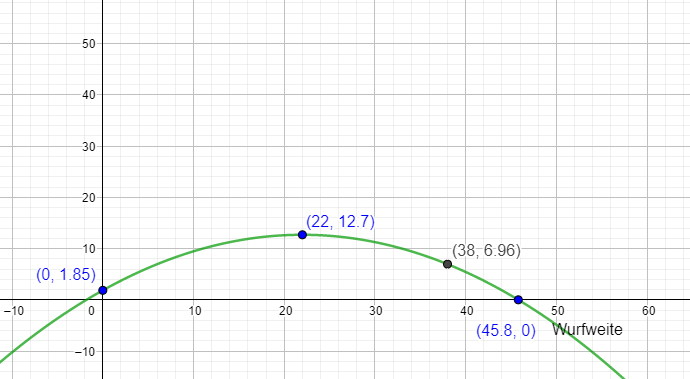
Den höchsten Punkt erreicht der Ball nach etwa 22 Metern in einer Höhe von 12,7m
\(f(x)=a(x-22)^2+12,7\)
Daniela wirft ihren Ball in 1,85m Höhe ab
Abwurf bei x = 0 in einer Höhe von y = 1,85
Diese Informationen (Koordinaten des Punktes (0 | 1,85) ) in die Gleichung einsetzen
\(1,85=a(0-22)^2+12,7\)
und nach a auflösen.
\(1,85=a(0-22)^2+12,7\\ 1,85=484a+12,7\\ -10,85=484a\\ -0,224\approx a\)
Somit lautet die Gleichung der Funktion \(f(x)=-0,224(x-22)^2+12,7\)
Um die Wurfweite zu bestimmen, musst du f(x) = 0 setzen und nach x auflösen.
c) Berechne f(38). Ist das Ergebnis größer als 3,2, fliegt der Ball über den Busch, sonst bleibt er hängen.
Gruß, Silvia