2.Berechnen Sie und zeichnen Sie ein:
a) den Benzinverbrauch nach 100 km in Liter
Berechne f(1). Zeichne einen Punkt auf der Kurve bei x=1.
3c) Berechnen Sie den durchschnittlichen Benzinverbrauch für die ersten 400 km in Liter pro 100 km und zeichnen Sie diesen in die Grafik ein!
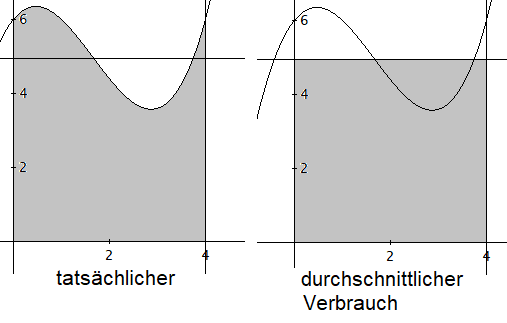
Der tatsächliche Verbrauch ist das Integral von f(x) in den Grenzen von 0 bis 4.
Der durchschnittliche Verbrauch ist das Rechteck rechts. Obere Begrenzung ist die Gerade y= der vierte Teil vom Integral von f(x) in den Grenzen von 0 bis 4.
Für Aufgabe 4 stelle eine neue Frage, bei der du nicht kopierts, sondern den Text über der Zeichnung und Aufgabe 4 abschreibst.