Bestimme mithilfe des GTR die Gleichung der Tangente im Punkt P(x0|f(x0)).

Question

Aufgabe:

Bestimme mithilfe des GTR die Gleichung der Tangente im Punkt P(x0|f(x0)). Gebe anschließend näherungsweise die Ableitung von f an der Stelle x0 an.

1. f(x) = 3 • √x; x0 = 4

2. f(x) 1/x - x^2; x0 = 0,5

Problem/Ansatz:

Beim ersten habe ich als Ableitung 0,75 raus und beim zweiten habe ich -5,  aber ich weiß nicht wie ich y mit dem GTR ausrechnen kann.

Comments

Wie heißt denn Dein GTR; bzw. wie ist seine Typ-Bezeichnung?

---

Classpad von Casio

Answer 1

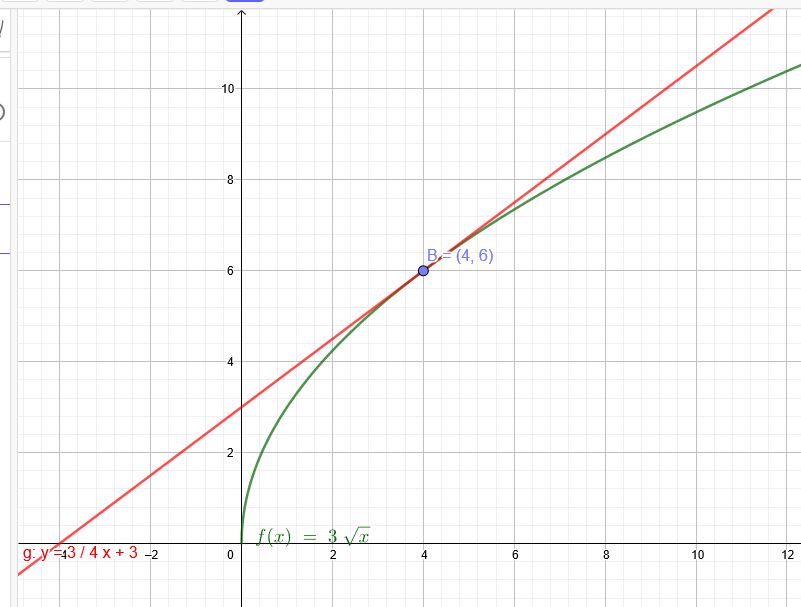
\(f(x) = 3 • \sqrt{x} \) ;  \(x₀ = 4\)   →       \(f(4) = 3 • \sqrt{4}=6 \)

\(f´(x) =\frac{3}{2 • \sqrt{x}} \)

\(f´(4) =\frac{3}{2 • \sqrt{4}} =\frac{3}{4}\)

Punkt-Steigungsform der Geraden:

\( \frac{y-y_1}{x-x_1}=m \) →    \(y=m•(x-x_1)+y_1 \) →    \(y=m•x-m•x_1+y_1 \)

\(B(4|6)\)

Tangente:

\(y=\frac{3}{4}•x-\frac{3}{4}•4+6=\frac{3}{4}•x+3\)

Answer 2

t(x) = (x-x0)*f '(x0)+ f(x0)

1. t(x) = (x-4)*f '(4) +f(4)

f '(x) = 3* 1/2*x^(-1/2) = 3/2*1/√x

2. f '(x) = -1/x^2 -2x

t(x) = ...