Berechne den Schnittwinkel für diese zwei Geraden

Question

Aufgabe:

Bestimme die Größe der Schnittwinkel der Geraden in Fig. 3 auf zwei verschiedene Weisen.

Problem/Ansatz:

Ich wollte mich einfach mal erkundigen, ob meine Lösung richtig ist: Ich habe durch die Differenz der Steigungswinkel gamma (Schnittwinkel)= 150,26°.

Diesen habe ich dann nochmal von 180° abgezogen, sodass ich dann ungefähr 29,74° raushabe.

Kann mir jemand bitte eine Rückmeldung geben, ob dies die richtige Lösung der Aufgabe ist? Vielen Dank :)

Comments

vgl:

https://www.mathebibel.de/lineare-funktionen-schnittwinkel-berechnen

Answer 1

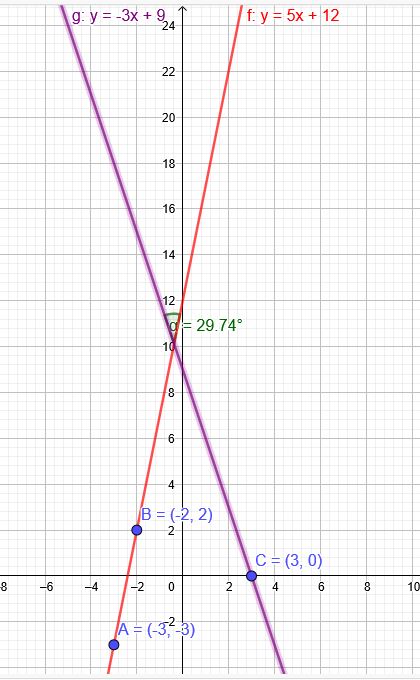
Lösungsweg mit der Schnittwinkelformel:

Steigung der Geraden durch $A(-3|-3)$und $B(-2|2)$

$m_1=\frac{2-(-3)}{-2-(-3)}=\frac{2+3}{-2+3}=5$

Steigung der Geraden durch $C(3|0)$und $D(5|-6)$

$m_2=\frac{-6-0}{5-3}=-3$

Winkel zwischen 2 Geraden:

$tan(α)=| \frac{m_2-m_1}{1+m_1*m_2} |$

$tan(α)=| \frac{-3-5}{1+5*(-3)} |=| \frac{-8}{-14} |=\frac{8}{14}=\frac{4}{7}$

$tan^{-1}(\frac{4}{7})=29,74°$

Answer 2

Ja, das ist korrekt.

Comments

Vielen, vielen Dank für Ihre Antwort!

Answer 3

Prima gemacht

ARCTAN(5) - ARCTAN(-3) = 150.26°

180° - 150.26° = 29.74°