Unter welchen Winkel sind die Seitenflächen zur Grundfläche geneigt?

Question

Aufgabe:

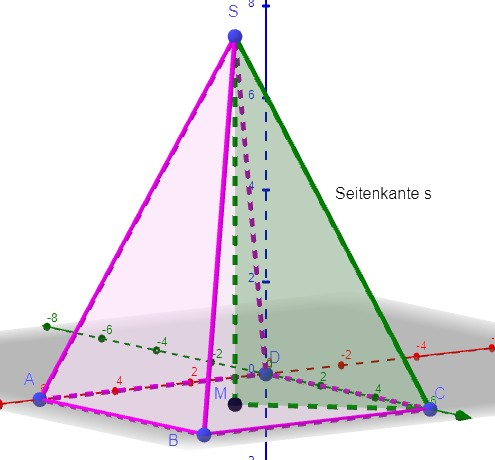
geg: quadratische Pyramide sind die Punkte A(6|0|0),B(6|6|0),C(0|6|0) und
S(3|3|8) (Spitze), D=(0;0;0)

c) Unter welchen Winkel sind die Seitenflächen zur Grundfläche geneigt?

wäre dankbar für jede Hilfe!!

Problem/Ansatz:

habe 9,06 für die Schenkellänge raus, da: |BS| UND |CS| =9,06

Ich weiss nicht was ich rechnen soll, den Winkel kann ich theoretisch mit meinem Geodreieck ausmessen, allerdings muss ich es nachvollziehen können

Answer 1

c) Unter welchen Winkel sind die Seitenflächen zur Grundfläche geneigt?

α = ARCCOS([0, 8, 3]·[0, 0, 1]/ABS([0, 8, 3])) = 69.44°

Es geht aber auch elementargeometrisch.

TAN(α) = 8/3 --> α = 69.44°

Comments

Oh man, Dankeeee!!! woher kommt die (0;0;1)? und was heisst ABS

---

ABS([0, 8, 3]) = √(0^2 + 8^2 + 3^2) ist der Betrag vom Vektor [0, 8, 3]

Der Vektor [0, 0, 1] ist der Normalenvektor der XY-Ebene. Du willst ja wissen wie die Ebene BCS gegenüber der XY-Ebene geneigt ist.

Answer 2

Hallo,

du kannst die Winkel zwischen zwei Vektoren, hier z.B. EM und ES mit der Formel

\( \cos (\alpha)=\frac{\vec{a} \circ \vec{b}}{|\vec{a}| \cdot|\vec{b}|} \) berechnen. Der Zähler ist das Skalarprodukt der Vektoren, der Nenner das Produkt ihrer Längen.

Melde dich, falls noch etwas unklar ist.

Gruß, Silvia

Comments

Danke!! es kommt bei mir 69,43 raus

---

Das Ergebnis vom Coach ist 69,44. Du hast vielleicht zu früh gerundet.