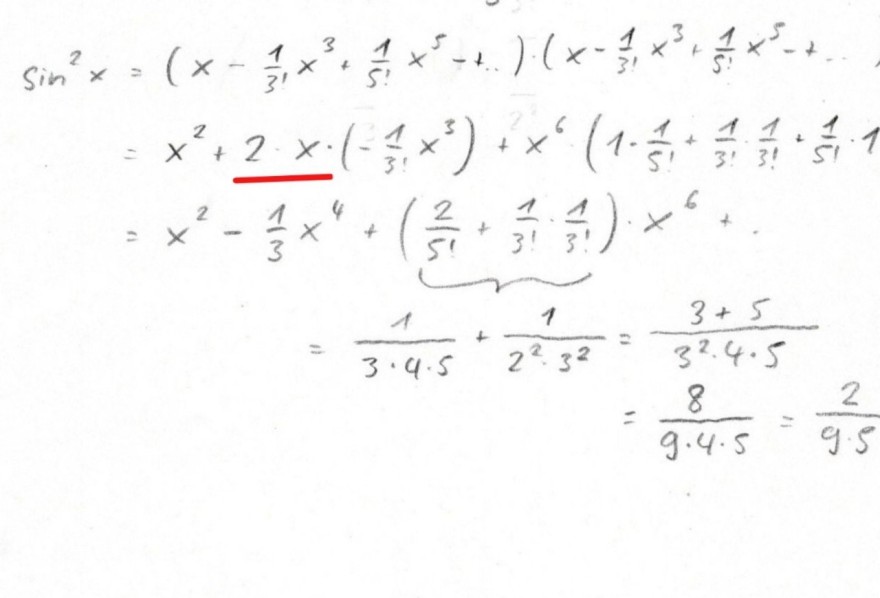Potenzreihenentwicklungen - Frage

Question

Wir sollen die Potenzreihenentwicklung aufschreiben, konkret die Koeffizienten ak, k = 0 ... 6 angeben.

Gegeben ist f(x) = sin²x

Frage ist jetzt, woher diese rot markierten 2*x im Bild herkommen? Egal, wie ich diese 2 gleichen Potenzreihen vom Sin. multipliziere, ich komme einfach nicht drauf!

Comments

Sollt ihr das tatsächlich per Multiplikation von Reihen machen?
Andernfalls empfehle ich \(\sin^2 x = \frac 12(1-\cos 2x)\).

Answer 1

Aloha :)

In deiner Rechung kommt der Term \(x\cdot(-\frac13x^3)\) zwei Mal vor, einmal in der Form \((-\frac13x^3)\cdot x\) beim 2-ten Summand der ersten Klammer und dem ersten Summand der zweiten Klammer und einmal in der Form \(x\cdot(-\frac13x^3)\) beim ersten Summand der ersten Klammer und dem zweiten Summand der zweiten Klammer. Daher der Faktor \(2\).

Die Darstellung ist richtig:$$\sin^2x=\frac12-\frac12\cos(2x)=\frac12-\frac12\left(1-\frac{(2x)^2}{2!}+\frac{(2x)^4}{4!}-\frac{(2x)^6}{6!}\right)=x^2-\frac{x^4}{3}+\frac{2x^6}{45}$$