Hallo,
mir ist nicht klar wie ich von der oberen Gleichung auf die untere komme:
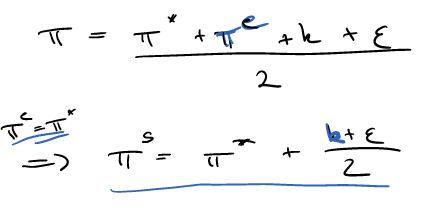
Pi = Inflation, Pi^e = erwartete Inlflation, Pi^* = optimale Inflation, Pi^s = surprise Lösung der Zentralbank, Epsilon = Angebotsschock, k = beliebige Variable
Könnte mir jemand die Umformungsschritte erklären die dazu nötig wären?
Danke und Gruß,
Daniel
Text erkannt:
\( \pi=\frac{\pi^{*}+\pi^{e}+k+\varepsilon}{2} \)
\( \stackrel{\pi^{2}=\pi^{*}}{\Rightarrow} \pi^{s}=\pi^{a}+\frac{k+\varepsilon}{2} \)