Aufgabe: Ermittle den Grenzwert der Folge, wenn an -> unendlich läuft
Problem/Ansatz:
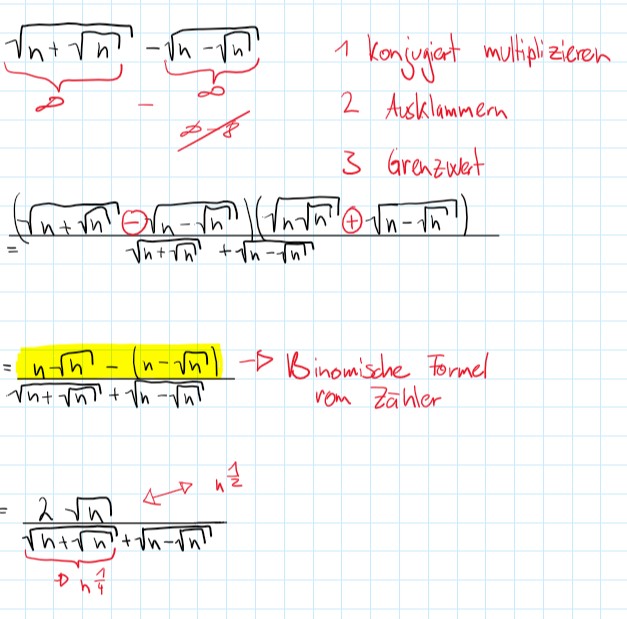
Text erkannt:
\( \begin{array}{l}\underbrace{\sqrt{n+\sqrt{n}}}_{\infty}-\underbrace{\sqrt{n-\sqrt{n}}}_{\infty} \quad 1 \text { konjugat multiplizieren } \\ 2 \text { Aukklammern } \\ 3 \text { Grenzwert } \\ =\frac{(\sqrt{n+\sqrt{n}} \theta \sqrt{n-\sqrt{n}})(\sqrt{n \sqrt{n}} \oplus \sqrt{n-\sqrt{n}})}{\sqrt{n+\sqrt{n}}+\sqrt{n-\sqrt{n}}} \\\end{array} \)
\( =\frac{2 \sqrt{n} \leftrightarrow n^{\frac{1}{2}}}{\sqrt{\sqrt{n+\sqrt{n}}}+\sqrt{n-\sqrt{n}}} \)
Leider komme ich nun nicht weiter. Wie würden die nächsten Schritte aussehen?